
这两天读了篇非常棒的论文,叫做Resample Importance Sampling,帮我弥补了许多概念上的漏洞
在这里我就读一遍8
本人也是学识有限,有错误麻烦Email告诉我...
对于一个总体(Population),我们可以从中抽取样本(Sample)$(X_1,X_2,X_3,....,X_N)$,该样本的样本容量(Sample Size)为N,其中$X_i$被称为随机变量(Random Variables),随机变量并不是一个值,他是一个从样本空间到实数集上的映射(或者说函数),而得到的实数值被称为观测值(Observation)
我个人的理解是,随机变量是个采样得到的值的容器,你可以多次采样,每次采样得到的结果被成为观测值,但采样这个过程本身是不确定的,所以随机变量的值随着每次采样而变,用计算机的概念来理解,var X = random();
估计量(Estimator)是一个关于随机变量的函数,他可以定义为如下:
$$
F_N = F_N(X_1,X_2,....,X_N)
$$
而$F_N$的具体数值被称为估计值(Estimate)。
我们比较熟知的估计量有最大似然估计,当然做为了解计算机图形学的壬,你也应该知道蒙特卡洛也是一个估计量。
当然对于计算机图形学来说,通常一个样本的样本容量为1,即$X_i$就是一个样本,那么N就是样本的个数了
对于一个有着数值解的函数$f(x)$,其积分形式为$I = \int_{\Omega}f(x)d\mu (x)$,其中$\Omega$为积分域。当f(x)没有闭式解或者说积分十分难计算的时候,就可以用蒙特卡洛方法求解。
蒙特卡洛的基本形式如下
$$F_N = \frac{1}{N} \sum^{N}_{i=1} \frac{f(X_i)}{p(X_i)}$$
其正确性不难验证,这里用期望(Expectation/Mean)的方法来证明,补充一下,期望可以认为是样本容量为无限大时的样本均值。证明如下
$$E(F_N) = E(\frac{1}{N}\sum^{N}_{i = 1}\frac{f(X_i)}{p(X_i)})$$
$$ =\frac{1}{N} E(\sum^{N}_{i = 1}\frac{f(X_i)}{p(X_i)}) $$
$$ =\frac{1}{N}\sum^{N}_{i = 1}({\int_{\Omega}\frac{f(x)}{p(x)}*p(x)d\mu (x) }) $$
$$ =I $$
除了排版不太好看以外,我保证其百分之百正确
所以只要样本足够多,$F_N$的均值就一定会给出正确的积分结果
接下来再探寻一些关于蒙特卡洛这个观测量的性质
为了遵循原文章,从此开始用Q代表积分的值。
我们把$F_N-Q$称为误差(Error),而误差的期望我们称为偏差(Bias)
$$\beta[F_N]=E[F_N-Q]$$
我们经常能在关于蒙特卡洛的文章中看到无偏性(Unbiased)这个词,一致性(Consistent)这个词却出现的很少。
那么什么是无偏性,一致性,又是什么使他们如此的重要?
如果一个统计量的偏差为0,我们称它具有无偏性
$$E[F_N] = Q\space for \space all \space N \geq1$$
更据之前的证明我们知道基本的蒙特卡洛是对积分的无偏估计量。
如果当样本容量趋向无穷,误差变为0,那么我们称这个估计量具有一致性。
$$\lim_{N\rightarrow+\infty}{F_N}=Q$$
通常来说,无偏的估计量也是一致的估计量。
对于无偏的估计量,我们可以轻松的计算出他的方差的估计值
令$Y_1,....,Y_N$作为一个无偏估计量$Y$的独立样本(注意此处是N个样本),并且令
$$F_N=\frac{1}{N}\sum^{N}_{i=1}Y_i$$
那么就有:
$$
\hat{V}[F_N] = \frac{1}{N-1}{(\frac{1}{N}\sum^{N}_{i=1}Y_i^{2}) -(\frac{1}{N}\sum^N_{i=1}Y_i)^2 }
$$
是对于$F_N$方差的无偏估计量
在渲染中,我们至少应该保证估计的一致性,尽量满足估计的无偏性。
因为无偏估计仅仅只需要计算其方差,并且能得到正确的结果;而对于有偏(但是一致的)估计你还得去限制他的偏差,偏差导致结果噪声多,而且不正确
增加样本量来减少其误差也可行就是....但是,代价是什么呢?
通常来说采样就是根据概率密度函数来生成样本,样本的分布应该贴合pdf。
约定一个符号$\xi$,代表从均匀分布$U[0,1]$中生成的一个随机数。
首先需要寻找一个简单的分布$q(x)$,令$p(x)<Mq(x)$成立,其中M是常数。
Step1. 对$q(x)$进行采样,得到样本$X_i$
Step2. 生成随机数$\xi$。
Step3. 若$\xi \le \frac{p(X_i)}{Mq(X_i)}$,那么返回$X_i$,反之拒绝$X_i$
拒绝采样牛在任何的分布都可以用这种方法采样,不过如果要提高采样效率,q(x)需要足够贴合p(x)
CDF,概率分布函数,cumulative density function,一般记作$F(x)$,且$F(x)=\int^{x}p(x')dx'$。
逆采样方法的原理基于CDF其实是一个在(0,1)上的均匀分布,证明如下
$F_X(x)=P\lbrace X\le x \rbrace=P\lbrace X\le F^{-1}_X(x)\rbrace=F_X(F_X^{-1}(x))=x$
得证。
那么进一步的,$F_X(X')=\xi$,那么$X'=F^{-1}_X(\xi)$
CDF的取值范围在(0,1)中且分布均匀,那么就均匀采样(0,1)再倒推其自变量。
这一结论可以推广至更高维度上,只需要计算边缘密度函数和条件概率分布再进行如上操作即可。
PMF,即离散概率密度函数。
采样PMF的方法比较简单,就是直接按pmf的比例进行采样。
这可能会遇到一点时间上的问题。。。可以用Alias法进行采样。
我感觉用不太上,不多描述了
混合分布就是把原来的分布按照一定权重$w_i$混合起来的分布,即$p(x)=\sum_{i=0}^{N}w_i*p_i(x)$。
采样的方法很简答单,首先依据权重的占比从N个分布中选择一个,接下来再采样选择的这个分布就行啦
其实就是采样PMF啦
Metropolis采样,其实就是马尔可夫链的应用blah,blah,不过我没学过,这里只能简述其过程了。。
这里有 好 东 西 https://zhuanlan.zhihu.com/p/146020807 ,可以康康
简单来说,Metropolis就是利用了马尔科夫链再经过一定的状态转移函数(或者提议分布;对于离散分布则是状态转移矩阵)之后会收敛到一个固定分布上(Stationary Distribution),而这个过程与初始状态无关,所以你可以选择一个简单的分布,采样一个复杂的分布。在此处,马尔科夫链的状态被简化到了两个:停留在当前点,和进入下一个状态(接受下一个样本)。
那么利用了这个采样方法的蒙特卡洛就是MCMC啦
接下来四具体步骤
Step1. 取一点$X$
step2. 从转移函数(或者说提议分布)$T(X|X^{i-1})$采样一个新点$X^{*}$
step3. 如果$\xi < min(1,\frac{\hat{q}(X^*)T(X|X^*)}{\hat{q}(X)T(X^*|X)})$,那么$X^i=X^*$,反之停留在该点。
step4. 把$X^i$加入样本堆里,回到Step2
还得提一句,马尔科夫链要进入稳定状态首先需要经过一段预热,在这期间,其样本需要丢弃,而这个预热的步长则需要经验来控制......
SIR,或者简称为Importance Resampling。
这种采样方法需要提供一个源分布q(或者叫Proposal Distribution?),和目标分布p
step1. 从源分布q中采样,得到M个样本$X_1,....,X_M$
step2. 计算权重$w_i=\frac{p(X_i)}{X_i}$
step3. 以权重$w_i$作为概率比例(probability proportional),对原来生成的样本进行有放回的抽样,生成N$(N\leq M)$个样本
这里的probability proportional我不知道如何翻译,应该就是靠权重进行离散分布函数的采样吧.....
这种采样方式允许从一个简单的pdf样本生成复杂的pdf的样本。
其中的源分布样本数M可以视作为一个插值量,如果当M=1时,那么最后样本的分布就是源pdf q的分布,随着M的增大,会越来越接近p的形状。
但也因如此,它生成的样本也只是近似于p。
原文中p是源分布,q是目标分布....
蒙特卡洛积分的方差的估计量为:
$$
V[F_N]=\frac{1}{N}V[Y]
$$
其中$F_N=\frac{1}{N}\sum^N_{i=1}Y_i$,而$Y_i=\frac{f(X_i)}{p(X_i)}$,$X_1,....,X_N$则是对$p(X)$采样得到的N个样本
证明:
$$
V[F_N] = V[\frac{1}{N}\sum^N_{i=1}Y_i]=\frac{1}{N^2}V[\sum^N_{i=1}Y_i]=\frac{1}{N}V[Y]
$$
那么显而易见的,此时方差只和$\frac{f(X)}{p(X)}$有关系,那么当$V[Y]$有限时,方差最终会随着样本量的增加而趋向于0。进一步得,减小Y这个比值可以使得相同得样本量下有着更小得方差。
这引出了重点采样,简单来说我们希望让项$f(X)$大的地方$p(X)$也大,反之则小,这就要求我们合适得选择一个pdf $p(X)$来贴合$f(X)$。
挑选的原则一般就是简单,方便采样。如果被积函数是一个乘积形式,那么可以选择其中的一项或者多项来挑选近似的pdf。
但是文章同时指出了一个问题:pdf需要针对不同的函数f分别选取,那么重要性采样方法不具备鲁棒性
嗯.....
简单来说把采样区域$\Omega$分成几个小片${\Omega_1,...,\Omega_N}$,然后对每个区域进行采样,进一步有分层采样蒙特卡洛估计:
$$
\int_{\Omega}f(w)dw\approx\sum^{N}_{i=1}\frac{f(x_i)}{p_i(x_i)}
$$
其中$p_i$是关于区域$\Omega_i$的pdf
原文说的是where pi is a probability density with support only in region Ωi 那么我猜这是一个条件pdf
重要性重采样就是用了SIR的蒙特卡洛...不
因为上文提到,sir生成的样本只是近似于目标分布P的分布,所以为了保持蒙特卡洛无偏性,需要加上一个权重项,于是有了如下
$$
\hat{I}_{ris}=\frac{1}{N}\sum^{N}_{i=1}\frac{f(y_i)}{\hat{p}(y_i)} \cdot w^{*}(X_1,...,X_M,Y_1,...,Y_N)
$$
其中$Y_i$是目标样本,$X_i$是提议分布生成的样本
在这里,$w^{*}=\frac{1}{M}\sum^M_{j=1}w(x_j)$
其中$w(x)$见前文SIR处
于是...
$$
\hat{I}_{ris}=\frac{1}{N}\sum^{N}_{i=1}(\frac{f(y_i)}{\hat{p}(y_i)}) \cdot \frac{1}{M}\sum^M_{j=1}w(x_j)
$$
到这里就可以列出RIS的步骤了
但是这种RIS估计存在缺陷,就是可能会重复采样同一个样本(因为目标样本是在提议样本中选取的),但是相同的样本不提供额外的信息,一个简单的解决是分层重要性重采样
对于提议分布q与目标分布p的选择遵从以下原则:
M,N的选择通过一个启发式来得到
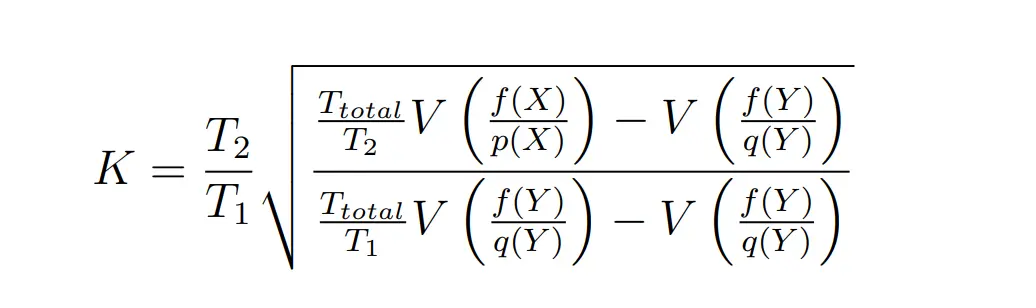
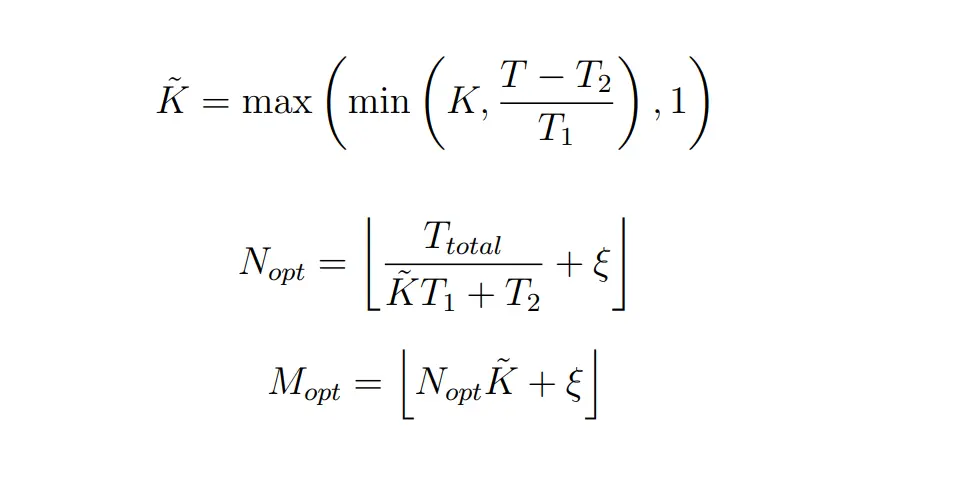
其中:T1+T2为总可用计算时间,T1是进行RIS 1,2步用时,T2是3,4用时
此处K可以用$K^*=\frac{T_2}{T_1}$来完成
在上面RIS的步骤上改进
而分层采样的RIS估计器是:
$$
\hat{I}_{ris_2}=\frac{1}{N}\sum^{N}_{i=1}(\frac{f(y_i)}{\hat{p}(y_i)} \cdot \frac{1}{M}\sum^{m_i}_{j=1}w(x_{ij}))
$$
假设有k个提议分布${q_1,...,q_k}$与目标分布p有着相同的积分域
从$q_i$中生成$m_i$个样本,再用MIS的启发式定义权重项
$$w(x_j)=\frac{m_i q_i(x_j)}{\sum^K_{k=1}m_k q_k(x_j)} \frac{\hat{p(x_j)}}{q_i(x_j)}$$
如果提议分布的定义域不同,那就不能像上文一样采样了...
不过还是可以把MIS用再样本上的
有一组K个采样分布,${\hat{p}_1,...,\hat{p}_k}$,用SIR对每个提议分布采样,这也表示需要RIS K次,每次产生$m_i$个提议样本和$n_i$个样本,并且$m_i$之和为M,$n_i$之和为N,然后用MIS启发式把样本组合起来,而且MIS的权重使用采样概率密度计算的,而不是提议分布的....
完啦 \( ̄︶ ̄*\))
博德之门3,启动!