不同BVH的构建策略

原创
飞起转圈
2024-07-22
529
计算机图形学

从根本上，BVH就是一颗二叉树，叶子节点有且仅有primitives，非叶节点则是其子孙的包围盒的Union。
当光线进入场景，首先需要和BVH的根做求交判断，如果命中，那么继续去其左右孩子节点做求交，如果命中，进入子树，如果没有命中，忽略其下面子树返回，可见这是一个递归的过程。
那么显然如何去构建这么一棵树 使得光线求交 递归访问的节点尽量的少 就成了最大的问题。

几种基础的BVH

1.最Naive的方法 ： 等分

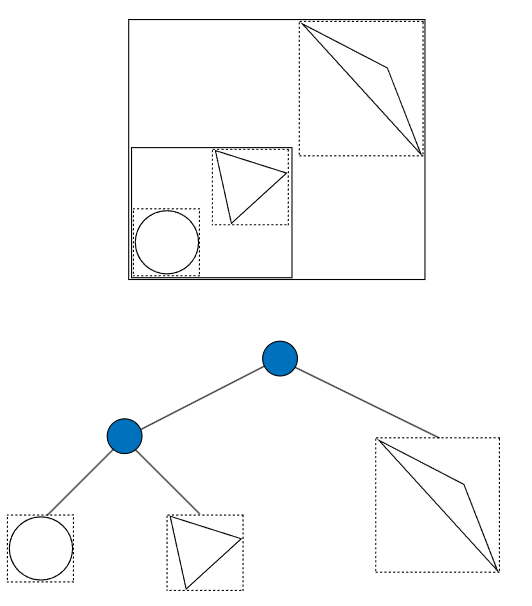
给入了一大堆的三角面，首先算他们AABB的Union，作为本节点的包围盒。
然后得到本AABB的长宽高，从中选取最长的一边，本次划分会在这个边所在的轴上进行。
在该轴上，对所有面进行排序，排序的Key就是面的中心坐标在划分轴上的分量。
接着，把这些面的前一半作为左节点，后一半作为右节点，继续本次递归过程。

伪代码：

Node(primitives) :
    if primitives.size < NodePrimitiveSize:
        this.primitives = primitives
        return
    aabb = new AABB
    for i in primitives:
        aabb.union(i.aabb)
    this.aabb = aabb
    axis = max(aabb.x,aabb.y,aabb.z)
    sort(primitives by axis)
    pLeft = primitives[0 to primitives.size() / 2]
    pRight = primitives[primitives.size() / 2 to primitives.size()]
    this.left = Node(pLeft)
    this.left = Node(pRight)

2.也很Naive的方法： 空间等分

上面的方法是在数量上等分，这种方法是在空间上的等分。

Node(primitives) :
    if primitives.size < NodePrimitiveSize:
        this.primitives = primitives
        return
    aabb = new AABB
    for i in primitives:
        aabb.union(i.aabb)
    this.aabb = aabb
    size = aabb.max - aabb.min
    axis = maxAxis(size)
    sort(primitives by axis)

    mid =  size[axis] / 2

    splitPoint = 0
    //二分法寻找中点，略...

    pLeft = primitives[0 to splitPoint]
    pRight = primitives[splitPoint to primitives.size()]
    this.left = Node(pLeft)
    this.left = Node(pRight)

3. SAH划分

SAH = Surface Area Heuristic 表面积启发式

上面两种方法属于：你说不出来哪不好，也说不出来哪好，也就是缺少了一个量化的标准。

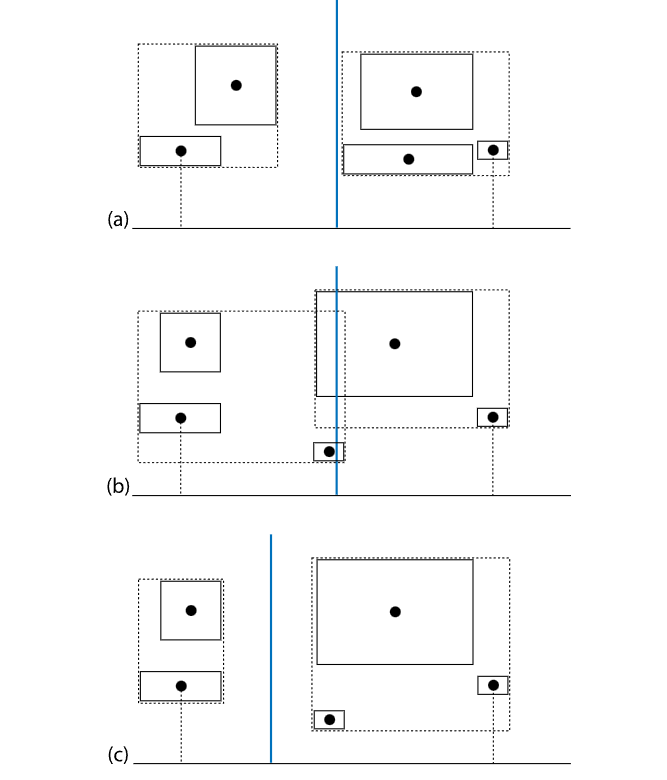
(a) 对于某种primitives的分布，选择了空间中点进行划分
(b) 新加入了一个primitive，依然利用中点进行划分 (c) 改用数量进行等分

比如说上图， 在(a)基础上增加了一个基元后分别用两种不同的策略进行划分的结果。
很明显(c)划分比(b)划分好很多，因为在(b)中，左右两个包围盒出现了重叠，这就说明：当光线求交时，它有更大的概率同时会击中两个包围盒，导致了一次额外的AABB求交，并且产生了一定的求交代价，如下：
$$ \sum^{N}_{i=1}=t_{isect}(i)
$$
其中N是节点中primitive的数量，$t_{isect}(i)$是对第i个primitive做求交所花费的时间。

所以，每次对BVH节点进行求交测试所花费的代价如下：
$$c(A,B) = t_{trav} + p_A\sum^{N_A}_{i=1}t_{isect}(a_i) + p_B\sum^{N_B}_{i=1}t_{isect}(b_i)$$
其中$t_{trav}$是每次遍历的时间花费，可以视作为一个常数，$p_A$是光线在击中了本包围盒后又集中了包围盒A的条件概率，同理$p_B$。
实际上$t_{isect}$也可以当作一个常数看待
于是经过了一番大型的简化后，问题就成了：如何使得
$$ c(A,B) =p_A + p_B $$
最小？

SAH方法中，我们让$p_A=\frac{S_A}{S_{node}}$，简单来说就是子节点的AABB表面积与本节点的AABB表面积之比。

首先，把要进行划分的轴在空间上均分为 n 段，，视为n个篮子，把primitive放进这些篮子里
随后，把篮子划成两批，分别作为左右子节点，计算cost，然后选择最小花费的那种划分。

伪代码如下：

Node(primitives) :
    if primitives.size < NodePrimitiveSize:
        this.primitives = primitives
        return
    aabb = new AABB
    for i in primitives:
        aabb.union(i.aabb)
    this.aabb = aabb
    size = aabb.max - aabb.min
    axis = maxAxis(size)
    sort(primitives by axis)

    const int nBuckects = 12 
    buckets[12]   

//初始化篮子   
    for i in primitives:
        b =nBuckets * aabb.Offset(i)[axis]
//往篮子里装primitives
        buckets[b].primitives += i
        buckets[b].aabb.union(i.aabb)
        buckets[b].counts += 1

    min_cost = MAX_INT
    split = 0
    for i = 0 to nBuckects - 1
        tmp_aabb_a = new AABB
        tmp_aabb_b = new AABB
        countA = 0
        countB = 0
        for j = 0 to i:
            tmp_aabb_a.union(buckets[j].aabb)
            countA = countA + buckets[j].counts
        for j = i to nBuckets:
            tmp_aabb_b.union(buckets[j].aabb)
            countB = countB + buckets[j].counts
        cost = .125f + countA * (tmp_aabb_a.area() / this.aabb.area())  + countB * (tmp_aabb_b.area() / this.aabb.area()) 

        if cost < min_cost:
            min_cost = cost 
            split = i
    primitivesA = buckets[0...split].primitives
    primitivesB = buckets[split...nBuckets].primitives
    this.left = Node(primitivesA)
    this.right = Node(primitivesB)

嗯..随手写的伪代码看看理解就好.....

总的来说，这种BVH确实会有更好的性能

可并行构建的BVH

LBVH

LBVH = Linear BVH 线性BVH

Linear BVH比较神奇的一点是利用了Morton code的Z curve特点。

Morton code就是把坐标的不同维度上的值错开，然后排列成一个二进制数（还是看图吧

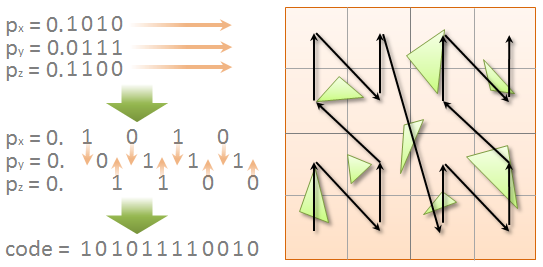
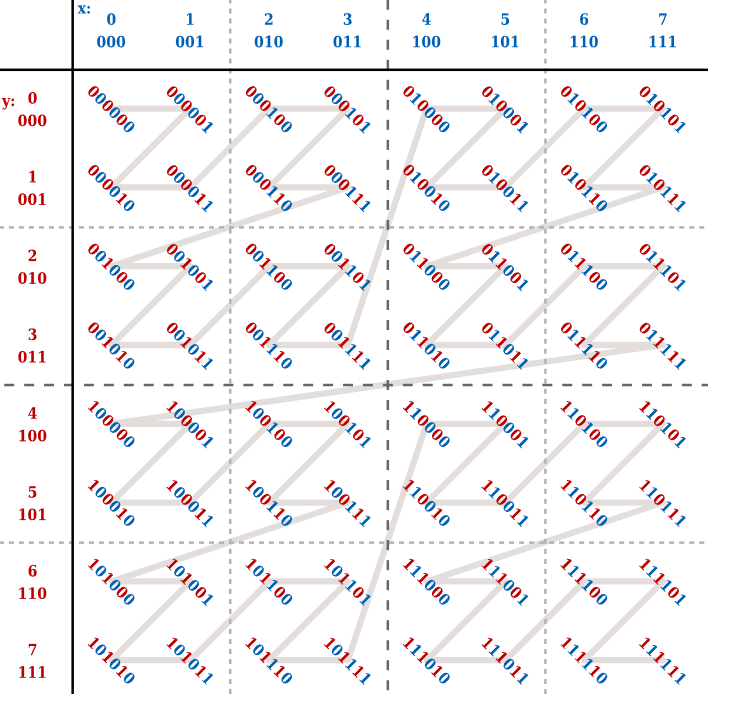
如图，就是一个y 一个x 一个y 一个x...这么排列!
然后对编码好的数字进行排序，你就会神奇的发现，在空间中相邻的点，竟然在morton code的排序中也是相邻的！
泰 神 奇 辣！

衍生到三维中，就好像给每块体素一个编码，相邻的体素在排序后以Z型被合成一块成了大体素，大体素也以相同的方式被合在一块....

于是就可以利用这个特点建树了....不对，怎么把现在的坐标转换为Morton code呢

Morton code Encode:


inline uint32_t LeftShift3(uint32_t x) {
    if (x == (1 << 10)) --x;
    x = (x | (x << 16)) & 0x30000ff;
    // x = ---- --98 ---- ---- ---- ---- 7654 3210
    x = (x | (x << 8)) & 0x300f00f;
    // x = ---- --98 ---- ---- 7654 ---- ---- 3210
    x = (x | (x << 4)) & 0x30c30c3;
    // x = ---- --98 ---- 76-- --54 ---- 32-- --10
    x = (x | (x << 2)) & 0x9249249;
    // x = ---- 9--8 --7- -6-- 5--4 --3- -2-- 1--0
    return x;
}

uint32_t EncodeMorton3(const Vector3f &v) {
    return (LeftShift3(v.z) << 2) | (LeftShift3(v.y) << 1) | LeftShift3(v.x);
}

可以发现一个很搞的问题：morton code好像是只能对uint编码啊？
实际上可以通过一点点小小Trick实现
简单来说就是先给一个浮点数放大一定倍数 ，然后再取整数算Morton Code

然后对于我这个文章的题目那后面必定是算...关于AABB中心点的morton，所以先把代码贴在这吧

Vector3 Offset(const Point3 &p) const {
    Vector3 o = p - pMin;
    if (pMax.x > pMin.x) o.x /= pMax.x - pMin.x;
    if (pMax.y > pMin.y) o.y /= pMax.y - pMin.y;
    if (pMax.z > pMin.z) o.z /= pMax.z - pMin.z;
    return o;
}

    //vector3 to morton 
    const int mortonScale = 10;
    Vector3f centroidOffset = bounds.Offset(primitiveInfo[i].centroid);
    mortonPrims[i].mortonCode = EncodeMorton3(centroidOffset * mortonScale);

好吧接着就该谈谈如何建树捏
首先需要计算每个Primitive的中心点的Morton code
然后再排序（用我之前发的方法就好捏( •̀ ω •́ )y）

那么如何划分呢？
简单来说就是找最长的公共二进制前缀，如果发现了不同的二进制位，那么就需要在这里进行划分，然后重复这个过程.....言语的描述还是太抽象了啊...看图！

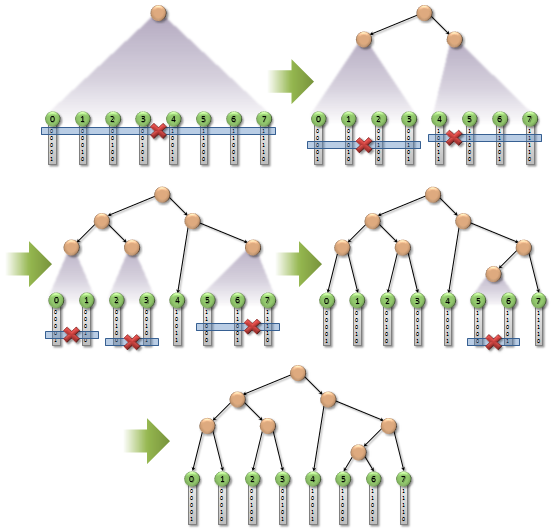
对于第一次划分，这8个数字并没有最长公共前缀，而且前四个数字和后四个数字第一位不同，于是从3号数字断开成两个节点；

第二次划分中前四个节点拥有最长公共前缀00，但是在第三位数字出现了不同的数，于是断开，对于后四个数字拥有共同前缀1，在第2位出现不同的数字，于是断开....总而言之就是这么来的！

int findSplit( unsigned int* sortedMortonCodes,
               int           first,
               int           last)
{
    // Identical Morton codes => split the range in the middle.

    unsigned int firstCode = sortedMortonCodes[first];
    unsigned int lastCode = sortedMortonCodes[last];

    if (firstCode == lastCode)
        return (first + last) >> 1;

    // Calculate the number of highest bits that are the same
    // for all objects, using the count-leading-zeros intrinsic.

    int commonPrefix = findMSB(firstCode ^ lastCode);

    // Use binary search to find where the next bit differs.
    // Specifically, we are looking for the highest object that
    // shares more than commonPrefix bits with the first one.

    int split = first; // initial guess
    int step = last - first;

    do
    {
        step = (step + 1) >> 1; // exponential decrease
        int newSplit = split + step; // proposed new position

        if (newSplit < last)
        {
            unsigned int splitCode = sortedMortonCodes[newSplit];
            int splitPrefix = findMSB(firstCode ^ splitCode);
            if (splitPrefix > commonPrefix)
                split = newSplit; // accept proposal
        }
    }
    while (step > 1);

    return split;
}

注意，findMSB是glsl的函数，代表着找到二进制中的第一个为1的位，在Cuda上完全可以用_clz来代替。。

但是这种自顶向下的方法还是没办法并行...

然而，有篇神奇的论文利用了二叉树的 非叶节点 = 叶子节点数量-1 特点，使得整棵树可以从下往上构建，使得其并行
如图：

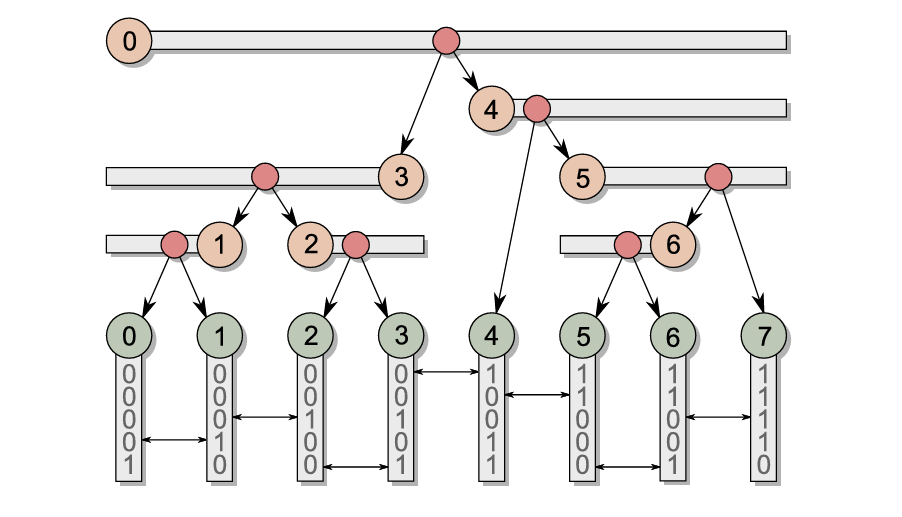
这棵树在文章中被称为Binary Radix Tree

算法的内容是通过观察到 首次发生最大公共前缀长度变化的地方一定是这棵树的节点分叉出子树的地方，作者巧妙的用子树的包含的叶子节点编号标记了节点，并且通过“方向”这个概念来标记子节点的范围。

再具体的讲解这个算法我也有点头大，看原文吧家人们

下文的代码是用来寻找树非叶节点的范围的

$\delta(x,y)$是求两个数的最长公共前缀个数，比如说对于上图的delta(0,1)就是3，如果数字超出了有效范围就返回-1
一个简单的实现如下：

int delta(int x, int y, int numObjects)
{
    if (x >= 0 && x <= numObjects - 1 && y >= 0 && y <= numObjects - 1)
    {
        const uint x_code = sortedMortonCodes[x];
        const uint y_code = sortedMortonCodes[y];
        // we guarantee that x_code != y_code
        return findMSB(x_code ^ y_code);
    }
    return -1;
}

还有个工程上会遇到的问题是：这篇文章中建BRT树需要独一无二的Morton code，但是primitive挨得很近难免会出现相同，此时算法中有个“方向”的计算就会失效（也就是伪代码中的d=0了，之后就没法进行计算），原文中的sec4惜字如金的提到了解决方法然而我没懂....
但是最简单的解决方法就是把 $$d\leftarrow sign(\delta(i,i+1) - \delta(i,i-1))$$
改为
$$d\leftarrow (\delta(i,i+1) - \delta(i,i-1)) > 0 ？ 1 ：-1$$
这样就work了....

在确定了节点对应的Morton code范围后，还需要通过找到范围的分割点来确定其左右孩子的编号
这一步也是通过二分法来寻找的
代码如下：

int FindSplit(int first, int last)
{
    const int commonPrefix = clz32(firstCode ^ lastCode);

    int split = first; 
    int step = last - first;

    do
    {
        step = (step + 1) >> 1; 
        const int newSplit = split + step; 

        if (newSplit < last)
        {
            const uint splitCode = sortedMortonCodes[newSplit];
            const int splitPrefix = clz32(firstCode ^ splitCode);
            if (splitPrefix > commonPrefix)
                split = newSplit; 
        }
    }
    while (step > 1);

    return split;
}

到这算是完全构建出来这颗“Binay Radix Tree”了。

接下来就是真正的BVH建树过程
作者提到的方法是为每个Primitive维护一个原子变量，每个线程负责一个Node，然后根据之前BRT的信息不停向上构建节点，如果当前节点的原子变量被标记为“来过”，那么就return。。。
这种策略不可避免的会导致最后线程利用率特别低就是了...

我承认这写的很乱...因为我也在实现，权当看个乐子吧QWQ

HLBVH

HLBVH的思想就是：在层数比较低的时候利用高质量的SAH来建树，但是在比较深的时候利用LBVH并行构建加快速度。

大体上分为几步：

  1. 计算所有primitive的AABB
  2. 计算所有primitive的Morton code
  3. Radix sort Morton code
  4. 创建LBVH的子树
  5. 从LBVH的子树中创建SAH BVH

其中1 2 3 能并行,4部分并行，5只能串行

对于4，其划分子树的做法就是拿当前节点的Morton Code与之前节点的Morton Code的高位做比较，如果相同就归到同一棵树上；反之则新开一颗子树，加入....有点像把树根削掉只留树干的感觉

代码如下：

std::vector<LBVHTreelet> treeletsToBuild;
for (int start = 0, end = 1; end <= (int)mortonPrims.size(); ++end) {
    uint32_t mask = 0b00111111111111000000000000000000;
    if (end == (int)mortonPrims.size() ||
                  ((mortonPrims[start].mortonCode & mask) !=
                   (mortonPrims[end].mortonCode & mask))) {
        int nPrimitives = end - start;
        int maxBVHNodes = 2 * nPrimitives - 1;
        BVHBuildNode *nodes = arena.Alloc<BVHBuildNode>(maxBVHNodes, false);
        treeletsToBuild.push_back({start, nPrimitives, nodes});
        start = end;
    }
}

这部分貌似只能串行

接着就是和构建LBVH一样的做法，只不过这次的输入分为好几部分的Primitives

进入第五步就是构建SAH BVH了，这部分的做法也和之前的构建SAH BVH一模一样，区别在于把Primitives换成了LBVH树而已....

目前看来，LBVH最适合用在实时渲染相关并且场景的变化特别大的地方，可以以很快的速度并行构建出来，但缺点是其质量不高
HLBVH则只能部分并行（当然这部分也可以送到GPU上做，然后取回做接下来的串行部分），构建效率还是差了LBVH一大截，但是质量高了不少，适合在CPU上的离线渲染，反复求交的收益会大很多。

对光线求交的优化

//由于我现在很困所以不写了Zzzz

Further Reading

[Karras 2012]提出了全并行GPU上BVH构建的仅仅是一颗低质量的LBVH树

为了进一步优化其性能，[Karras 2013]又提出了一种：先构建一颗低质量的树，然后再调整树的拓扑结构来提升树质量的方法

END