最近在读pbrt和rt gem，发现在重要性采样这块一堆半球采样，球采样。这让我这个高数1.6的学渣很烦，没办法，从头开始。
圆心角从高中到大学一直见到，设在二维平面的单位圆弧上取一处弧微分记为 $ds$，那么可以定义$d\theta = \frac{ds}{r}$（想想弧长公式）。
对圆心角在$\lbrace0,2\pi\rbrace$上积分，因为圆的周长为$2\pi r$，可得$\int_{0}^{2\pi}{d\theta} =\int_{0}^{2\pi}{\frac{1}{r}ds=2\pi}$
那么在三维上与圆心角对应的就是立体角了。设在单位球上取一处面积微元$dA$，维度上升了，分母自然变成了$r^2$，则可以得到$d\omega = \frac{dA}{r^2}$，由于球的表面积为$4\pi r^2$,同理对立体角的积分可得到为$4\pi$。
立体角的单位为$sr$, 中文叫球面度。
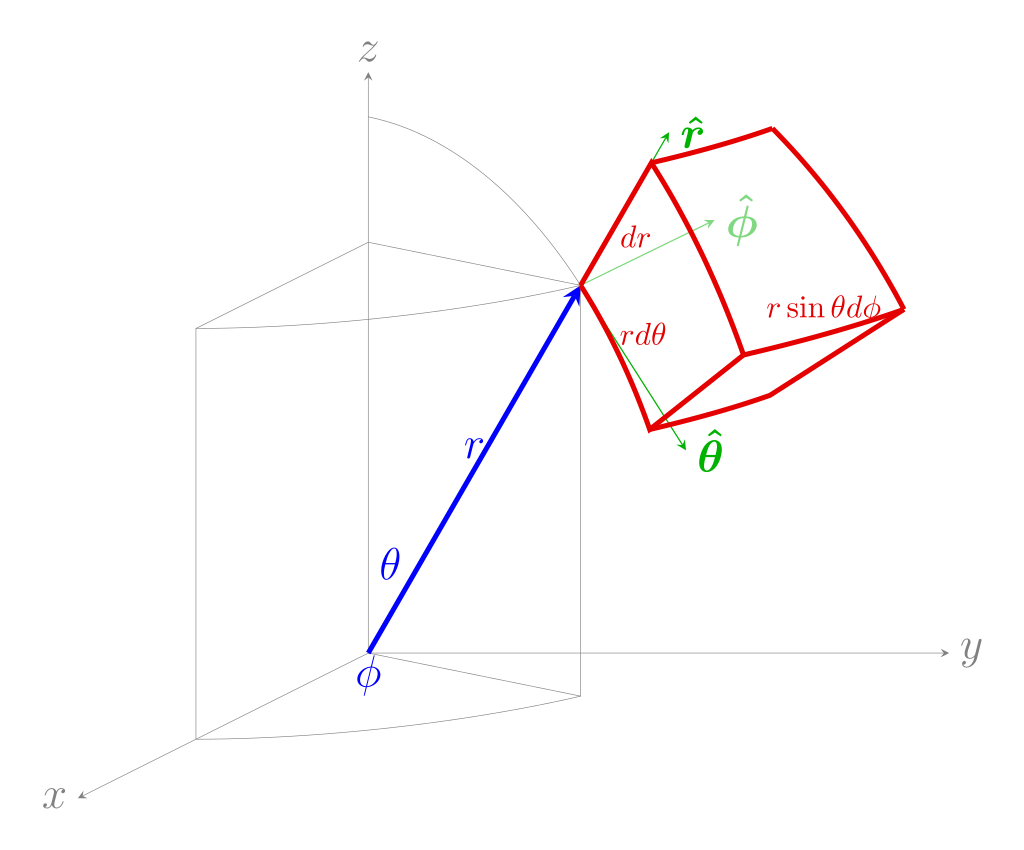
刚学三重积分的时候可能会遇到对球的体积进行积分这样的题，在不知道任何其他知识的情况下，我们会选择对$dx,dy,dz$依次积分，但是我们可以通过把对$dx,dy,dz$的积分换成在球坐标下对$dr,d\theta,d\phi$的积分。如图
根据一点点三角的知识，我们可轻松得到以下表达：$z=rcos\theta,x=rsin\theta cos\phi ,y=rsin\theta cos\phi$。简单计算可以得到$\theta=arccos\frac{z}{r},phi=arctan\frac{y}{x}$.
再进一步，我们可以得到对于体积元素的等式$dv=r^2sin\theta drd\theta d\phi$。
对于面积元素，$ds=r^2sin\theta d\theta d\phi$。
有了图推导很简单，其实就是把dv或者ds拆成几条边相乘，稍微想一下就出来了。
有了面积微元的球面座标表示，再根据上一部分所说的立体角定义，那我们又可以得到立体角与$\theta,\phi$的关系，$d\omega = sin\theta d\theta d\phi$
至此，我们完成了从三重积分到立体角的火箭跳！
其实在图形学中，我们一般都会使用单位球，这样上文中无数的r都可以变为1，这样一来又简单了很多，而立体角其实也就是定义在单位球上的一块面积。
这一篇我似乎讲的不是很明白，逻辑也十分的跳跃。而且受制于本人水平，如有错误，劳烦指出！