受制于本人水平，文章难免有误，望能指出，感激不尽。

Perlin Noise

简介

Ken Perlin在1983年开发了Perlin Noise并且在1985年的Siggraph提出，算是一项“古老的技术”了。
Perlin Noise适合用来做程序化的内容生成，比如说Minecraft里的地形生成，电影里的火焰特效等等...

算法

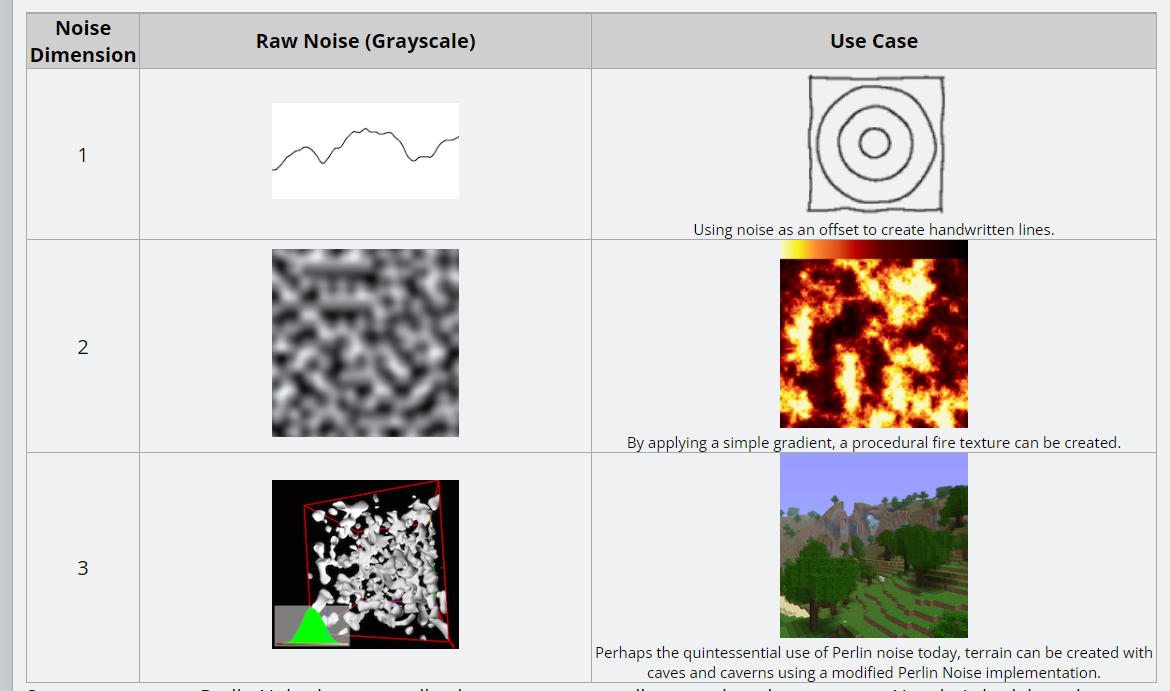
这个Perlin Noise可以实现在一维，二维，三维甚至更高维的噪声，其时间复杂度为$O(2^n)$
这里主要讲的是二维的Perlin Noise
首先，在空间上做一个划分，形成格子结构，构成这个格子的其实就是空间中每个点的整数部分。对于一个格子的四个顶点（三维就是8个点），赋予一个固定的随机梯度向量（Gradient Vector）。

还需要得到距离向量，就是从格子的四个顶点分别指向目标点的向量。

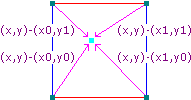
接着把对应的距离向量和梯度向量进行点乘。
由于梯度向量的长度越大，它对结果的影响也越大，为了避免这种情况的发生，需要对梯度向量进行归一化。
接下来需要对点乘得到的四个值使用缓和曲线（ease curve,也可以叫fade function）进行插值。
在最早的论文中，这个缓和曲线是$s(t)=3t^2-2*t^3$，到了2002年的论文中改进成了$s(t)=6t^5-15t^4+10t^3$。

关于这个缓和曲线有点讲究...首先，这个曲线是穿过所有格子顶点的Hermite样条，需要在格子顶点处(t=0,t=1)的导数具有连续性。比如最开始的 $s(t)=3t^2-2*t^3$ 是个三次Hermite样条，其一阶导在t=0,t=1处都是0，但是二阶导数在顶点处不连续。与之相对，五次样条$s(t)=6t^5-15t^4+10t^3$则没有这个问题，他在t=0,t=1处的一阶导，二阶导都为0。

好吧，我上面写的东西可能有点不知所云，但是下面的代码不会骗人。

实现

这部分是噪声函数的核心代码

float noise(const vec2& p) {
	vec2 pi{ float(int(p.x)), float(int(p.y)) };
	vec2 pf = p - pi;
	vec2 fade = easeCurve(pf);
	float AP = pf.dot(
		hash2(pi)
	);
	float BP = (pf - vec2{ 1, 0 }).dot(
		hash2({ pi.x + 1, pi.y })
	);
	float CP = (pf - vec2{ 1, 1 }).dot(
		hash2({ pi.x + 1, pi.y + 1 })
	);
	float DP = (pf - vec2{ 0, 1 }).dot(
		hash2({ pi.x, pi.y + 1 })
	);
	float k = lerp(
		lerp(AP, BP, fade.x),
		lerp(DP, CP, fade.x),
		fade.y);
    //k in (-1,1)
	return  k * 0.5 + 0.5;
}

这是个我从Wiki上扒来的Hash函数，其返回值已经被归一化过了。

这代码实在是...看不太懂，玩Shader的数学神仙太多了...

vec2 hash2(vec2 pi) {
	// No precomputed gradients mean this works for any number of grid coordinates
	int ix = pi.x;
	int iy = pi.y;

	const unsigned w = 8 * sizeof(unsigned);
	const unsigned s = w / 2; 
	unsigned a = ix, b = iy;
	a *= 3284157443; b ^= a << s | a >> w - s;
	b *= 1911520717; a ^= b << s | b >> w - s;
	a *= 2048419325;
	float random = a * (3.14159265 / ~(~0u >> 1)); // in [0, 2*Pi]
	vec2 v;
	v.x = cos(random); v.y = sin(random);
	return v;
}

在经典版和2002的Perlin Noise实现中，有一个Permutation数组，里面放的是0-255数字的重排序，用来作为hash函数的随机种子，这保证了每个梯度向量都互不相同...但是用点的坐标直接也不是不行，所以就不需要啦
这个permutation数组放在下面以供观瞻

int permutation[] = { 151,160,137,91,90,15,
   131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
   190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
   88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
   77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
   102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
   135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
   5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
   223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
   129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
   251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
   49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
   138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
   };

其他的变形

噪声函数可以通过组合来形成其他不同的噪声
比如说fbm（Fractal Brownian Motion），可以把不同频率的noise按照不同振幅混合起来。表达式如下：
$\sum\frac{2^inoise(V)}{2^i}$
写成代码也简单

float noise_sum(const vec2& p, int layer) {
	float a = 1, f = 1;
	float value = 0;
	for (int i = 0; i < layer; i++)
	{
		value += a * noise(p * f);
		f = f * 2;
		a = a * 0.5;
	}
	return value;
}

还有给其他的变形，我只给表达式，就不贴代码了
$\sum|\frac{2^inoise(V)}{2^i}|$

$sin(x+\sum|\frac{2^inoise(V)}{2^i})|$