
结于2022/9/18,勿忘国耻。
我在刚入门图形学时就曾听说过IQ大神的牛逼,怀着朝圣的心情打开Shadertoy膜拜了他的几个作品...没有模型,没有顶点,只靠数学函数来构建一个虚拟的世界,甚至做出动画,难以置信。可惜当时的我被满屏幕的数学公式吓到了,只留下了个赞就跑了。


IQ大神作品
这个月我又打开了shadertoy,里面的数学公式晦涩依旧,但是我好像有了一丢丢挑战它的信心(被PBRT虐出来的蜜汁自信
总之,我记下这篇文章作为我对shaderToy中Ray marching和SDF的学习笔记。我会尽量用我的理解方法来解释,尝试用简单的方法来说明(尽管里面充斥着各种不科学的解释,民科的思路blablabla...)。如果文章有哪部分开始变得语焉不详、不知所云,也请理解,我可怜的大脑已经尽力了(ToT)/~~~
在被shader折磨之前先来首音乐\( ̄︶ ̄*\))
遇到不会的不要慌,We are only human.
开始吧!
SDF,signed distance field,中文为有向距离场,它的作用就是储存空间中点到物体的最短距离。因为是有向,所以在物体内部的点其sdf的值为负数,在外部的点sdf的值为正。

模型有显式和隐式表示方法。显式模型表示方式有三角网格、曲线或者点云。隐式的模型则可以通过SDF表示,一般需要配合上Ray marching来渲染。
除此以外,SDF也能表示2D的物体。V社就曾经提出过用SDF来渲染字体。传统的贴图字体在放大后会出现锯齿或者模糊,而SDF字体因为具有矢量性显得更加平滑。
一个最简单的SDF例子:球
$x^2 + y^2 + z^2 = 1$
代码:
float sdfSphere(vec3 p){
return length(p) - 1.0;
}
在下一部分我会把这个球渲染出来。
Ray Marcing,光线步进,乍一听名字会让人想到邪恶的光线追踪,他们确实有很多相似点:比如说在一开始都得选一个相机的位置,然后找到光线射出的方向。

from < ray tracing in one weekend >
首先,先为相机找到个位置,然后在其面前放上一个网格,这就是一个成像平面,上面的每一个格子都是一个像素。简单点,可以把它想象成你面前的屏幕,而你就是那个相机。所有物体都得先显示在屏幕上,才能被你看到。
首先需要知道平面的高度长度,然后还得知道相机的fov。有了这些就能计算光线方向了。
相机被放在了成像平面的中间,光线从相机射出,朝着成像平面上的每一个格子去...那么平面上的点减去相机的位置就是光线方向了..等等,相机位置的z值是多少?
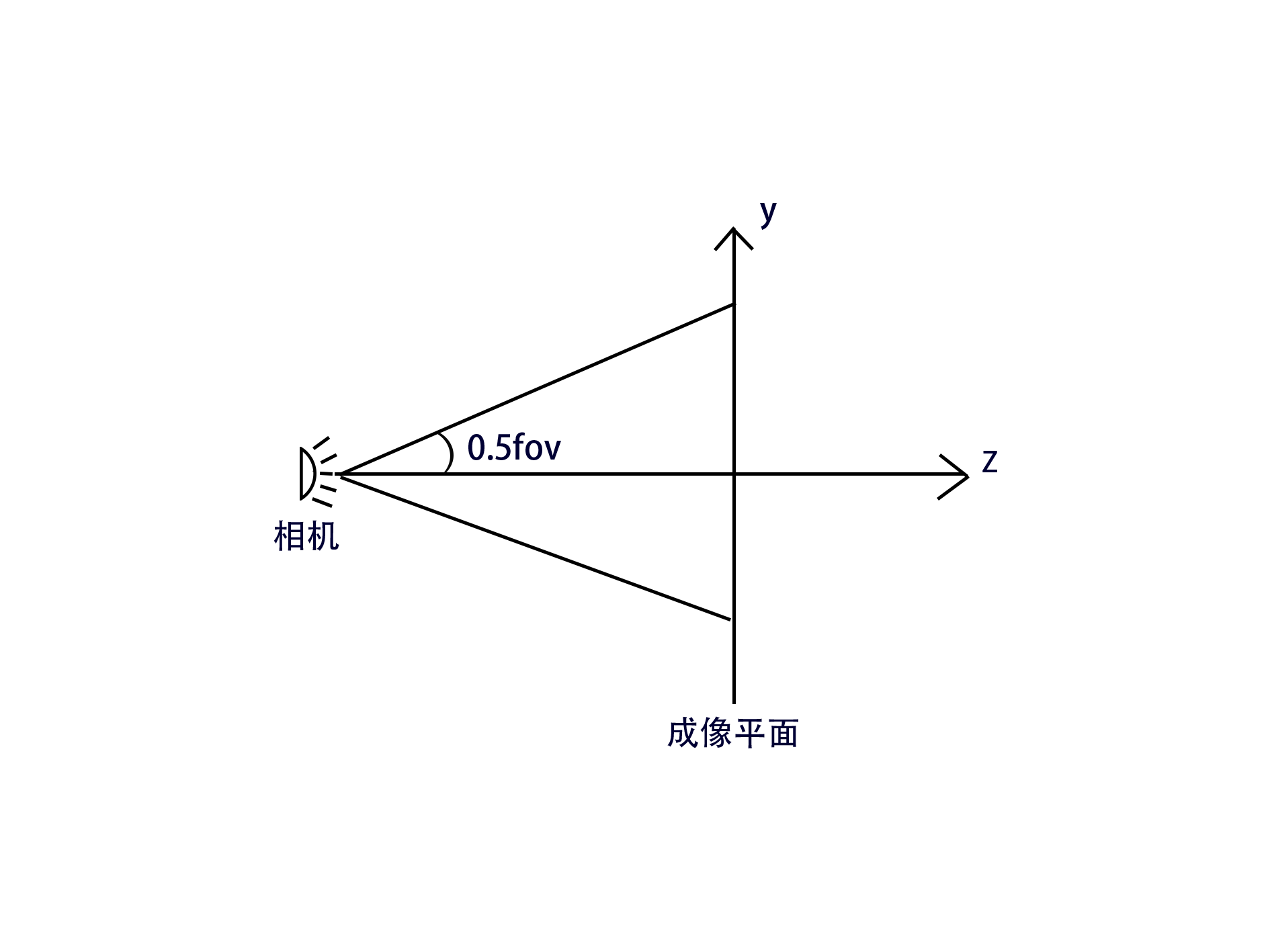
如图ヾ(^▽^*)))
得到$z=\frac{y}{2}/tan(\frac{fov}{2})$
由此可以发现fov越大光线散射的越开,视角也越大,fov越小,光线越集中,看到的也越少。有点像焦距hhhh
vec3 getRay(float fov_degree,vec2 fragCoord,vec2 imgSize){
vec2 img_center = imgSize / 2.;
float z_cam = ((imgSize.y/2.)/tan(radians(fov_degree)/2.));
return normalize(vec3(fragCoord,0.) - vec3(img_center,z_cam));
}
现在正式进入Ray marching了
光线步进,正如其名,光线每次行进一段距离。传统的Ray Marching算法中,光线行进的长度固定,如果打到物体,那么就采用二分法或者牛顿迭代寻找光线与物体的交点,伪代码
step = 0.1
ray = eyePos
for i in range(0,step_max):
ray +=direction*step
if hit:
findRoot
这种方法效率低下,很容易错过微小的物体,迭代次数需要很大.....
在gpu gems2里,提到了一种新的算法,球体追踪(Sphere Tracing)

其方法就是,每次迭代之前先通过SDF得到与物体的最短距离,然后把这个距离作为光线接下来行进的长度。那么,在离物体远的时候,光线就行进的块,离得近的时候行进的慢,迭代次数大大减少。更妙的地方在于,由于SDF是该点到物体的最近距离,所以每次行进的距离都是一个“安全长度”,光线永远不会错过物体。
const float eps = 0.00001;
const int STEP_MAX = 32;
float rayMarching(vec3 eye,vec3 dir,float start,float end){
float depth = start;
for(int i = 0 ;i < STEP_MAX;i++){
vec3 p = vec3(eye + dir * depth);
float dist = map(p);
//当与物体离得非常非常近了
//认为打到了物体
if(dist < eps){
return depth;
}
depth += dist;
if(depth > end){
return end;
}
}
return end;
}
这里的map当然是上一部分的那个球球了
float sdfSphere(vec3 p){
return length(p) - 1.0;
}
float map(vec3 p){
return sdfSphere(p);
}
然后就可以算出交点,渲染物体
const float MIN_DEP = 0.001;
const float MAX_DEP = 30.0;
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec3 dir = getRay(45.,fragCoord,iResolution.xy);
float rayDepth = rayMarching(vec3(0,0,5),dir,MIN_DEP,MAX_DEP);
//如果没打中物体,那么返回黑色
if(rayDepth > MAX_DEP - eps){
fragColor = vec4(0,0,0,1.0);
}
else{
fragColor = vec4(1,0,0,1.0);
}
}

芜湖~
回忆一下高等数学,有个概念叫梯度,表示某一函数在该点处的方向导数沿着该方向取得最大值,在P点的梯度记作$\triangledown f(p)$,其计算方法就是分别对x,y,z求偏导数,可以写为$\triangledown f(p)=(\frac{\delta f}{\delta x}(p),\frac{\delta f}{\delta y}(p),\frac{\delta f}{\delta z}(p))$。对于SDF函数,其在p点的梯度就是法线。
简单的证明一下:
设一个SDF函数$f(p)=0$,那么其在P点的切线可以表示为$(dx,dy,dz)$
通过全微分的定义可得到:
$\frac{\delta f}{\delta x}dx+\frac{\delta f}{\delta y}dy+\frac{\delta f}{\delta z}dz=0$
$\Rightarrow \triangledown f(p)\cdot (dx,dy,dz)=0$
得证。
虽然有了求解析解的方法,但是对于计算机来说,求导数无疑是艰难的任务...那么,必须要舍弃解析解,转而寻找一个数值解。
最简单的方法无疑是采样,但是思想仍然未变
vec3 radient(vec3 p){
return normalize(
vec3(
map(vec3(p.x + eps,p.y,p.z)) - map(vec3(p.x - eps,p.y,p.z)),
map(vec3(p.x,p.y + eps,p.z)) - map(vec3(p.x,p.y - eps,p.z)),
map(vec3(p.x,p.y,p.z + eps)) - map(vec3(p.x,p.y,p.z - eps))
));
}
但是,在IQ大神的博客里,提到过一种性能更加优秀的方法,四面体技术(Tetrahedron technique)。我先把代码放上来
vec3 calcNormal( in vec3 p ) // for function f(p)
{
const float h = 0.0001; // replace by an appropriate value
const vec2 k = vec2(1,-1)*0.5773;
return normalize( k.xyy*f( p + k.xyy*h ) +
k.yyx*f( p + k.yyx*h ) +
k.yxy*f( p + k.yxy*h ) +
k.xxx*f( p + k.xxx*h ) );
}
这种方法只需要采样四次!相比之前的方法快了1/3。但是,这东西就像magic,和之前的理论完全不一样....好吧,我会顺着IQ大神的思路复述一遍,顺带着加入点我的理解。
这种方法把采样的点换成了一个四面体的四个顶点:$k0 = (1,-1,-1), k1 = (-1,-1,1), k2 = (-1,1,-1),k3 = (1,1,1)$。
考虑一下这个公式
$m=\sum_{i}k_if(p+hk_i)$
可以进行如下变形
$m=\sum_{i}k_i(f(p+hk_i)-f(p))$
ps:能这么干的原因是$\sum_ik_i*f(p)=(0,0,0)$
这可以视为求四个点沿着方向ki的 方向导数!(如果在这有疑惑就看看wiki吧,这是上面的公式哦)
又因为,梯度点乘方向的单位向量就能得到方向导数,所以上面的式子又可以继续改写为
$m=\sum_ik_i \triangledown_{k_i}f(p)=\sum_ik_i(k_i\cdot \triangledown f(p))$
注意:这里第一个$k_i$是逐分量相乘(aka.哈达玛积)。
最后一步了,把四个点带进去,直接硬算,然后就会发现结果是 $4*\triangledown f(p)$
最后归一化就能得到法线了!!!!
最后最后一点,有人可能疑惑:向量k为什么要乘以0.5773?
这不是magic number,是1/sqrt(3),对|ki|这个向量归一化。因为
梯度点乘方向的 单位向量 就能得到方向导数

百试不爽的normal shader
在获得法线之后,实现光照几乎不存在难度了。
Blinn-Phong作为一个古老的光照模型应该也是人尽皆知了吧
直接放代码
/*
* n -> normal
* p -> fragPos
* lp -> lightPos
* sn -> shiness
* lc -> lightColor
*/
vec3 blinnPhong(vec3 n,vec3 p,vec3 lp,vec3 eye,vec3 kd,vec3 ks,vec3 lc,float sn){
vec3 lightDir = lp - p;
float light_normal_cos =max(dot(normalize(lightDir),n),0.);
vec3 diffuse = light_normal_cos * lc * kd;
vec3 half_vector =normalize(normalize(eye - p) + normalize(lightDir));
float cos_h_n = max(0.,dot(half_vector,n));
vec3 specular = pow(cos_h_n,sn) * ks * lc;
return diffuse + specular;
}
vec3 illumination(vec3 k_a, vec3 k_d, vec3 k_s, float sn, vec3 p, vec3 eye){
vec3 lightColor = vec3(.7,.75,.88);
//ambient
vec3 color = k_a * lightColor;
vec3 normal =normalize(calcNormal(p));
vec3 ligPos = vec3(5.*sin(iTime),3. , 5.*cos(iTime));
color +=blinnPhong(normal,p,ligPos,eye, k_d,k_s,lightColor,sn);
return color;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec3 eye = vec3(0,0,5);
vec3 dir = getRay(45.,fragCoord,iResolution.xy);
float rayDepth = rayMarching(eye,dir,MIN_DEP,MAX_DEP);
if(rayDepth > MAX_DEP - eps){
fragColor = vec4(0,0,0,1.0);
}
else{
vec3 p = eye + dir * rayDepth;
vec3 clr = illumination(vec3(.1), vec3(.5,.4,.7), vec3(.9,.9,.9), 32., p, eye);
fragColor = vec4(clr,1.0);
}
}
结果:
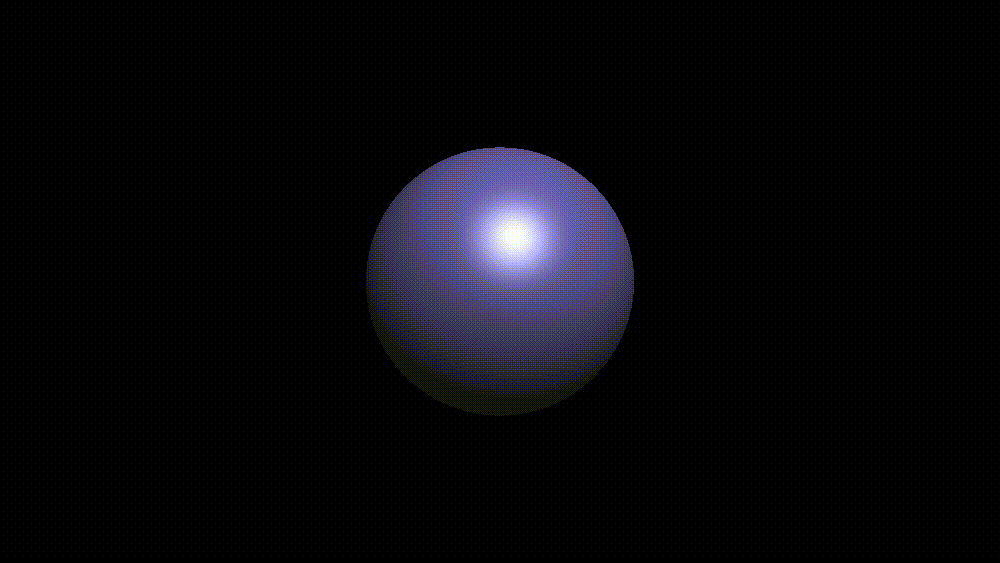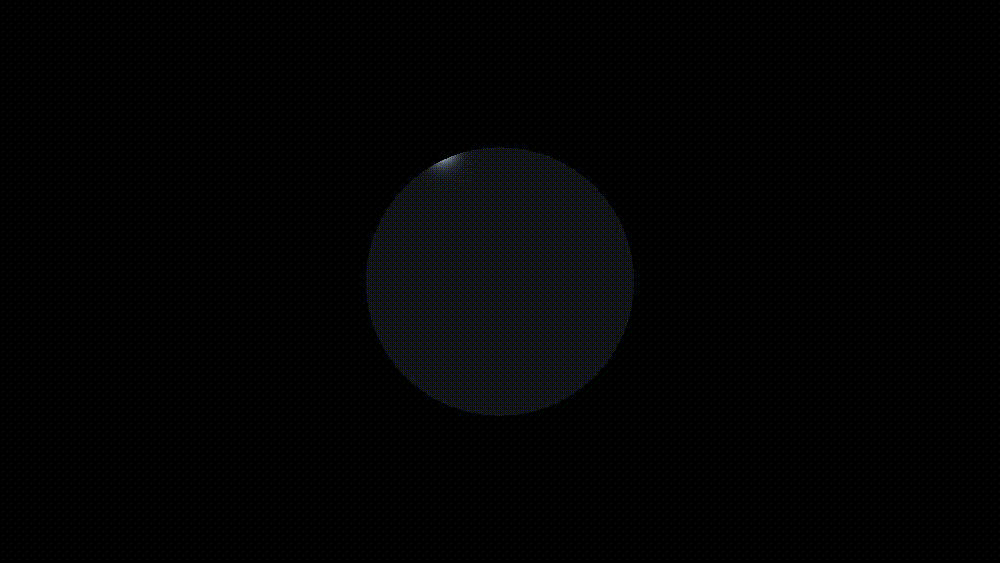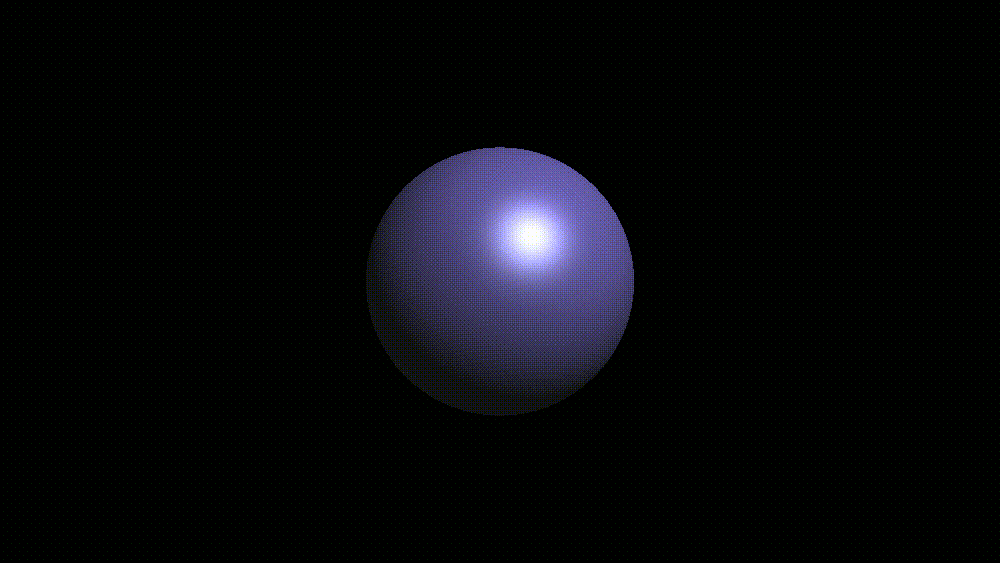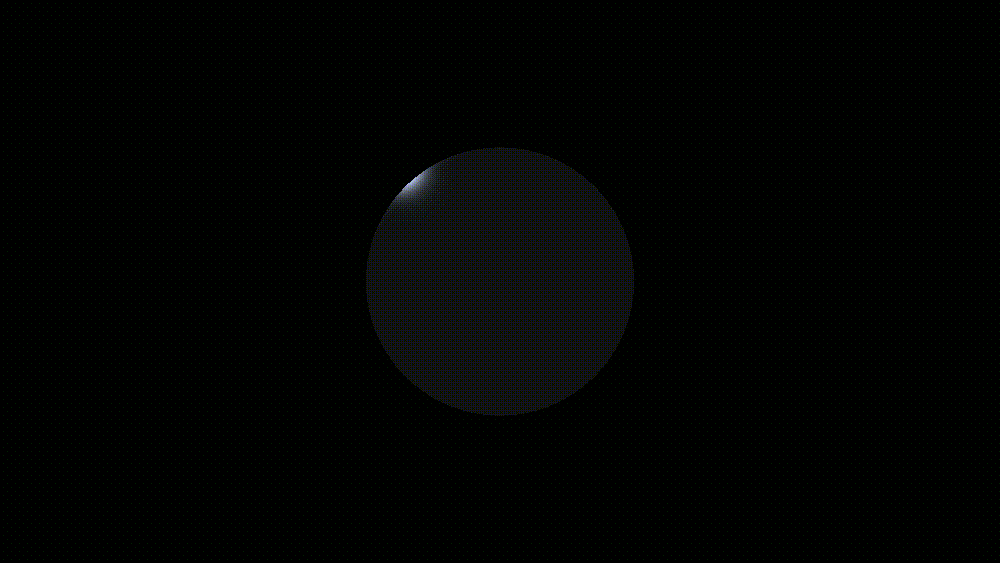
如果想要实现多光源也不难,只需要把光照计算的结果相加就行了..
其实从第一次渲染出那个红色的球开始,我就受不了这该死的锯齿了
抗锯齿的方法很简单,就是超采样。多射出几根光线,每根光线加入微小的偏移,最后把得到的颜色总和求平均。
![]()
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec3 eye = vec3(0,0,5);
vec3 clr = vec3(0);
for(int j = -1;j<=1;j+=2){
for(int i = -1;i<=1;i+=2){
vec3 dir = getRay(45.,fragCoord+vec2(i,j)/3.,iResolution.xy);
float rayDepth = rayMarching(eye,dir,MIN_DEP,MAX_DEP);
if(rayDepth < MAX_DEP - eps){
vec3 p = eye + dir * rayDepth;
clr += illumination(vec3(.1), vec3(.5,.4,.7), vec3(.9,.9,.9), 32., p, eye);
}else{
clr +=vec3(0);
}
}
}
fragColor = vec4(clr/float(4),1.0);
}
放一张对比图,左边是AA处理过的,右边没有。可以看到左图确实少了点毛刺

对于一个光追器,移动摄像机,其实就是是移动光线的行进方向
当然,对光线步进也是同理,只需要一个观察矩阵就行啦
这里直接参考glu的实现,推导(我)不(会)重要
第一个参数是相机的位置,第二个参数是看向的位置,第三个参数是相机的上轴(一般是(0,1,0))
mat4 viewMat(vec3 eye,vec3 lookAt,vec3 up){
vec3 w = normalize(lookAt - eye);
//Mind the order of cross product
vec3 u = normalize(cross(up,w));
vec3 v = normalize(cross(w,u));
return mat4(
vec4(u,0.),
vec4(v,0.),
vec4(-w,0.),
vec4(0.,0.,0.,1.0)
);
}
当然我也准备了点参考文章放在这里
Understanding the View Matrix
然后把光线的射出方向乘以这个矩阵就大功告成啦
该做点演示了(* ̄3 ̄)╭
但是....球从哪面看都是圆的,这样很难进行展示啊......
所以我要引入一个新的SDF物体: >CUBE<
float cubeSDF(vec3 samplePoint){
vec3 p2surf = abs(samplePoint) - vec3(.5,.5,.5);
float outsidePointLength = length(max(p2surf,0.));
float insidePointLength = min(max(max(p2surf.x,p2surf.y),p2surf.z),0.);
return outsidePointLength+insidePointLength;
}
float map(vec3 p){
return cubeSDF(p);
}
这是一个边长为1的正方体,至于为什么我下章会说~
然后咱让相机绕着立方体转起来
vec3 eye = vec3(5. * sin(iTime),0,5.*cos(iTime));
mat4 mView = viewMat(eye,vec3(0,0,0),vec3(0,1,0));
vec3 dir = getRay(45.,fragCoord,iResolution.xy);
dir = (vec4(dir,1.) * mView).rgb;

是否感觉眼花缭乱?接下来还有呢,比如滚筒机动
vec3 eye = vec3(0,0,3);
vec3 up = normalize(vec3(sin(iTime),cos(iTime),1.));
mat4 mView = viewMat(eye,vec3(0,0,0),up);
由于上轴代表了相机的上方在哪,所以只需要让上轴转起来,相机就能做滚翻了。

在这一部分开始前,建议去看一下IQ大神的这篇博客-distance functions,很多SDF不用自己计算,可以直接COPY他的。
我在这里会写几种常见的SDF函数,都是我自己上手推过的哦~
首先是个球,$P^2-R^2=0$。
那么如果想要改变球的位置,那就相当于移动球心,于是也可以这么写
$(P-O)^2-R^2=0$
float sdfSphere(vec3 p,float r){
return length(p) - r;
}
float map(vec3 p){
vec3 spherePos = vec3(1,1,1);
float r = 1.;
return sdfSphere(p - spherePos,r);
}
平面就是在某一个维度上无限延伸的面
比如说最常见的,在y=k上的一个平面可以表示为$p.y - k$
float SDFPlane(vec3 p){
return p.y;
}
float map(vec3 p){
//在y=0上的平面
return SDFPlane(p);
}
在IQ大神的博客里还有一种更好的平面SDF函数,能表示所有的平面 - 只需要那个平面的法线
float sdPlane( vec3 p, vec3 n, float h ){
// n must be normalized
return dot(p,n) + h;
}
n一定要归一化!!!
这个函数也不难理解,就是把点P视作了从原点出发的向量,而dot(p,n)则是把这个向量投影到了法线方向上并算出长度。
其中h应该是平面到原点的距离。
但是这些函数都只能表示在相机下方的平面,如果要得到一个在相机上方的平面,需要在结果上加个绝对值~
Box的SDF函数稍微难理解一点点....
Box的SDF函数分成了两部分,第一部分是当点在box外边时点和box表面的距离,另一部分则是当点在box里面时点和box表面的距离。
float cubeSDF(vec3 p,vec3 c){
vec3 p2surf = abs(p) - c;
float outsidePointLength = length(max(p2surf,0.));
float insidePointLength = min(max(max(p2surf.x,p2surf.y),p2surf.z),0.);
return outsidePointLength+insidePointLength;
}
这是一个以2倍c的各分量为边长的一个Box。
这种表示方法的缺点是只能表示轴对齐的Box,不过不急,接下来我会给出解决方法。
去看IQ大神的这篇博客-distance functions
人生苦短,我用轮子啊( ´・・)ノ(._.`)
首先是和运算
float unionSDF(float a,float b){
return min(a,b);
}
一个盒子和一个球合在一起

然后是交运算
float intersectSDF(float distA, float distB) {
return max(distA, distB);
}

最后就是求异运算
float differenceSDF(float distA, float distB) {
return max(distA, -distB);
}

球-box
上面三种就是最基本的运算了。
但是,这里的求交运算求出来图形有点太生硬了,好像是盒子上莫名凸出来了一块,这时候就需要一个平滑求交函数,让球和盒子存在一些过渡
float smin( float a, float b, float k )
{
float h = max( k-abs(a-b), 0.0 )/k;
return min( a, b ) - h*h*k*(1.0/4.0);
}

感觉有点邪典..
到目前为止,所有物体都安安静静的呆在(0,0,0)上...这也太无聊了..
如何让物体动起来?
可以像传统的渲染一样,使用模型矩阵来完成物体的旋转移动和缩放,不过在这里还需要把矩阵求逆。
伪代码如下
vec3 opTx( in vec3 p, in mat4 t, in sdfFunction sdf )
{
return sdf( inverse(t)*p );
}
构建模型矩阵的函数我会放在本章的最后....因为这并不是这里的重点,在Fragment Shader里算矩阵的开销太大了!!!!求逆和算矩阵相乘非常非常复杂。
幸好,这里还有其他的方法。
可以换个思路,不用移动模型,可以移动采样点。
对于位移操作来说,如果把模型往右移动五个单位,其实可以等价于把采样点左移5个单位。

于是可以这样操作:
vec3 opTranslate( in vec3 p, in vec3 offset, in sdfFunction sdf )
{
return sdf( p - offset );
}
这种方法计算量少了很多,而且实现起来也很简单
但是对于模型缩放,就不能简单的把点除以缩放系数了
考虑一个球$x^2+y^2+z^2=1$,把球缩小一倍,那么缩放系数为0.5,如果简单的把采样点除以采样系数,那么这个函数等价为 $distance=\sqrt{4x^2+4y^2+4z^2}-1$,对于点(0.5,0,0)返回值为0,正合我意。但是对于(1,0,0),其返回值为1,而正确的返回值应该为0.5。在哪里出错了么?实际上,除以了缩放系数相当于对整个空间进行了一个缩放,如果要得到正确的返回值,还得对结果乘以缩放系数来还原空间。
vec3 opScale( in vec3 p, in float s, in sdfFunction sdf )
{
return sdf(p/s)*s;
}
但是注意,这个方法只适用于等比缩放。
万一只想让物体的某一个轴上缩放,那么也可以进行类似的操作,先把采样点在每个轴上除以缩放系数。但对于得到的结果,需要乘以这个三维的缩放系数中最小的那一维度。
因为如果乘上了其他较大的维度,会导致空间被过度放大,得到的距离就会变大,可能导致Ray Marching错过目标物体!
vec3 opScale( in vec3 p, in vec3 s, in sdfFunction sdf )
{
return sdf(p/s)*min(min(p.x,p.y),p.z);
}
对于旋转操作,确实没有很好的办法,还是得用上矩阵。但大部分的时候,我们只是想让物体沿着某条坐标轴转动,于是可以单独写出绕x,y,z轴转动的矩阵,这样可以可以减少几次三角函数的计算..
// Rotation matrix around the X axis.
mat3 rotateX(float theta) {
float c = cos(theta);
float s = sin(theta);
return mat3(
vec3(1, 0, 0),
vec3(0, c, -s),
vec3(0, s, c));
}
// Rotation matrix around the Y axis.
mat3 rotateY(float theta) {
float c = cos(theta);
float s = sin(theta);
return mat3(
vec3(c, 0, s),
vec3(0, 1, 0),
vec3(-s, 0, c));
}
// Rotation matrix around the Z axis.
mat3 rotateZ(float theta) {
float c = cos(theta);
float s = sin(theta);
return mat3(
vec3(c, -s, 0),
vec3(s, c, 0),
vec3(0, 0, 1));
}
最后一个很常用的,就是无限重复。无限重复操作特别简单,就是取余,而被取余的数字就是重复的区间。但是在取余后一定要把点换入关于轴对称的坐标系中 - 除非你只想要半个物体。
vec3 opScale( in vec3 p, float c, in sdfFunction sdf )
{
//Repeat on x axis
return sdf(vec3(mod(p.x)- 0.5*c,p.y,p.z) );
}
还有许多操作,像对称,扭曲.....等等等等,看IQ大神的博客吧!

在一个光滑的平面上,一堆诡异的盒子自西向东无限延申,盒子仿佛飘在空中,因为.....它们没有影子!
下一部分实现一个高效的软阴影ヾ(•ω•`)o
旋转矩阵位移矩阵以及缩放矩阵,还有个很hack的绕轴旋转函数erot
mat4 translate(vec3 delta){
return mat4(
vec4(1,0,0,0),
vec4(0,1,0,0),
vec4(0,0,1,0),
vec4(delta.x,delta.y,delta.z,1));
}
mat4 scale(vec3 delta){
return mat4(
vec4(delta.x,0,0,0),
vec4(0,delta.y,0,0),
vec4(0,0,delta.z,0),
vec4(0,0,0,1));
}
mat4 rotate(vec3 axis,float theta_rad){
axis=normalize(axis);
float cos_theta=cos(theta_rad);
float sin_theta=sin(theta_rad);
return mat4(
vec4(axis.x*axis.x*(1.0-cos_theta)+cos_theta , axis.y*axis.x*(1.0-cos_theta)+axis.z*sin_theta, axis.z*axis.x*(1.0-cos_theta)-axis.y*sin_theta , 0.0),
vec4(axis.x*axis.y*(1.0-cos_theta)-axis.z*sin_theta, axis.y*axis.y*(1.0-cos_theta)+cos_theta , axis.z*axis.y*(1.0-cos_theta)+axis.x*sin_theta, 0.0),
vec4(axis.x*axis.z*(1.0-cos_theta)+axis.y*sin_theta, axis.y*axis.z*(1.0-cos_theta)-axis.x*sin_theta, axis.z*axis.z*(1.0-cos_theta)+cos_theta , 0.0),
vec4(0.0 , 0.0 , 0.0 , 1.0));
}
vec3 erot(vec3 p, vec3 ax, float ro) {
return mix(dot(ax, p)*ax, p, cos(ro)) + cross(ax, p)*sin(ro);
}
注意,旋转矩阵和erot旋转都是以 过原点的直线为旋转轴 。而且erot函数里的ax(也就是旋转轴)必须被归一化。那如果旋转轴不过原点怎么办呢?这就必须先把旋转轴的起点移动到原点,然后再把物体做相应的位移,然后再进行计算,最后再把结果移动回去,有点绕啊....
那这个erot函数到底是啥嘞?
好吧,其实就是罗德里格斯旋转公式,只不过代码真的太™hack了....hack爆了。我是手动把算式展开了一下..然后突然联想到了....
中文互联网上唯一一个关于erot函数的讲解竟然要付费开专栏才能看,而我这免费的一下就说出来了,是不是很超值啊哈哈哈哈哈
那在RayMarching中,如果想实现一个位置在pos的盒子绕着自身的y轴旋转,那么应该这么做:
float dist = Box( erot(p - pos,vec3(0,1,0), radians(theta) ) );
这里的p-pos可以理解为把物体的坐标移动回了模型坐标系(也就是以自身的中心为原点的坐标系),然后再以y轴为旋转轴进行旋转。
我为啥要说这么多呢? 因为我在这里翻车过.......
阴影是一个重磅话题....但是,SDF阴影很简单
先从SDF硬阴影开始实现。
一般来说,阴影形成的原因,就是光源发出的光线被遮挡,因而照射不到目标。
但是我们可以反向思考,比如说,从着色点往光源看,如果在着色点看不到光源,那么说明光线不能照射到着色点。用这个思路,可以从着色点往光源的方向进行光线步进,查找障碍物
float calcSoftShadow(vec3 ro,vec3 rd,float tMin,float tMax){
//when obj is above the light
if(tMax < 0.){
return 0.;
}
for(float t = tMin;t < tMax;){
float h = SDFScene(ro + rd * t);
//if ray hits obstacle
if(h < 0.0001){
return 0.;
}
t +=h;
}
return 1.;
}
--------
//in render function
float visibility = calShadow(ro,rd,0.001,t_from_p_to_light);
color *= visibility;

这个阴影是不是还行啊哈哈哈哈
理想的点光源会造成硬阴影,但是在现实生活中,大部分的光源都是面光源,所以会产生一些虚化的过渡,这种不黑不亮的地方被称作半影(Penumbra)
吐槽一下,国内有些翻译软件会把Penumbras翻译成愁云..我寻思着是不是lol打多了
模拟这种虚化的方式很多,比如古老的PCF,PCSS技术,还有VSM之类的

我在MC里做的PCSS嘿嘿
但是,我在这里要讲的是SDF软阴影,先讲一下它的原理。
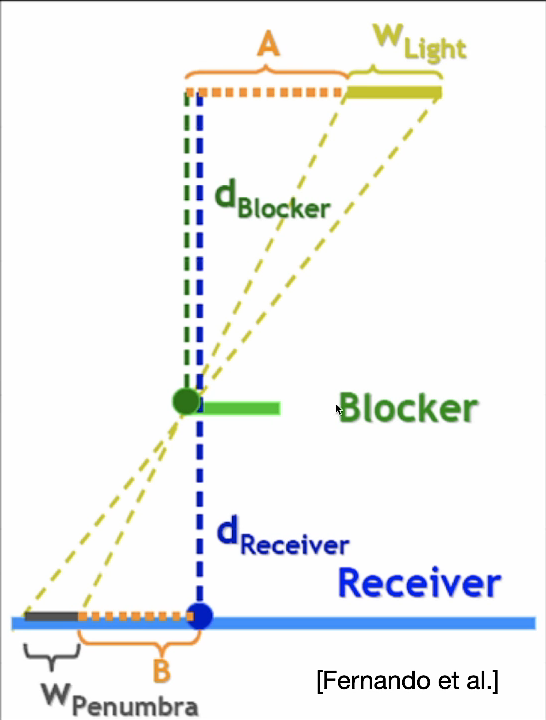
其实很简单,寻找光线两侧最近的障碍物,然后可以想像一根线正好和这个障碍物相切。那么光线和与障碍物相切的线的夹角大小就可以表示半影,比如说如果两根线的夹角在0-20°就存在半影,而大于20°就没有半影,完全可见....

from games202
那么如何求这个角度大小呢?其实不用精确的求出来,只需要大概知道这个比例就行,用采样点与物体的最近距离比上光线行进的路程,再用一个系数控制半影的大小就行了惹,所以表达为(k*h/t)
float calcSoftShadow(vec3 ro,vec3 rd,float tMin,float tMax){
float res = 1.0;
for(float t = tMin;t < tMax;){
float h = SDFScene(ro + rd * t);
res = min(res,5.*h /t);
t +=h;
if(res < 0.01 || t > tMax){
break;
}
}
clamp(res, 0., 1.);
return res * res * (3. - 2.*res);
}
最后又对结果做了一次插值,但我觉得没啥必要...直接返回res也行

但是,有些时候物体的阴影会出现条状...很明显是不对的

球的阴影出现了明显的条状
出现这种条状artifacts是因为光线在行进的途中错过了与SDF的最近点。
对此,有一项改进,那就是把对SDF最近的距离的采样位置放在...呃..还是看图吧
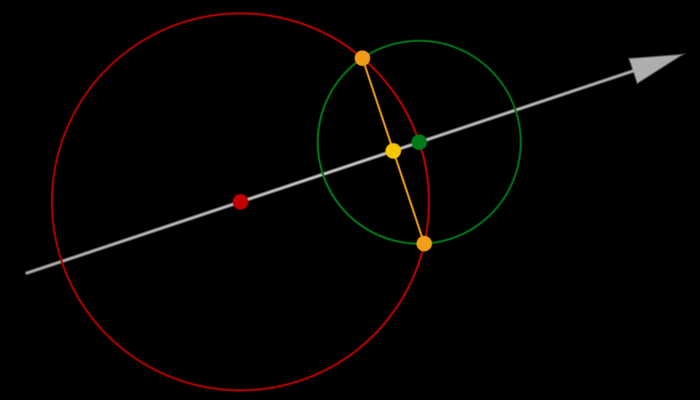
对,把这个位置放在橙色的点位,那么设橙色线段长度的一半为y,绿色点到橙色线段的最近距离 为d,那么我们的软阴影评估式就变成了:k*y/(t-d) 。而且,根据图上可以看到,y/(t-d)其实就是tan..
求y和d也十分简单,只要用到三角比例....
第一个球的半径为r1,第二个的为r2:
$\frac{r_2}{2r_1}=\frac{y}{r_2}$
$y=\frac{r_2^2}{2r_1}$
$d=\sqrt{r_2^2-y^2}$
//code from https://www.shadertoy.com/view/lsKcDD
float softshadow( in vec3 ro, in vec3 rd, float mint, float maxt, float k )
{
float res = 1.0;
//big, such that y = 0 on the first iteration
float ph = 1e20;
for( float t=mint; t<maxt; ){
float h = map(ro + rd*t);
if( h<0.001 )
return 0.0;
// use this if you are getting artifact on the first iteration, or unroll the
/ first iteration out of the loop
//float y = (i==0) ? 0.0 : h*h/(2.0*ph);
float y = h*h/(2.0*ph);
float d = sqrt(h*h-y*y);
res = min( res, k*d/max(0.0,t-y) );
ph = h;
t += h;
}
return res;
}

改进后的场景虽然还是有一丢丢的artifact,但好歹能看得过去了不是
AO,就是环境光遮蔽,在WIKI上是这么解释的:
环境光遮蔽(英语:ambient occlusion)是计算机图形学中的一种着色和渲染技术,用来计算场景中每一点是如何接受环境光的。
在很多游戏中也能看到关于AO的画质选项,比如HBAO,SSAO,还有非常新颖的VXAO等等。
不过这里提到的是基于SDF的一种AO,一种简单的近似
这个算法是我在IQ的一个博客里发现的,后面又看到了他的代码。
这种算法的大概思路就是沿着表面的法线对SDF进行多次采样,如果发现有物体遮蔽,那么就在这点产生环境光遮蔽。
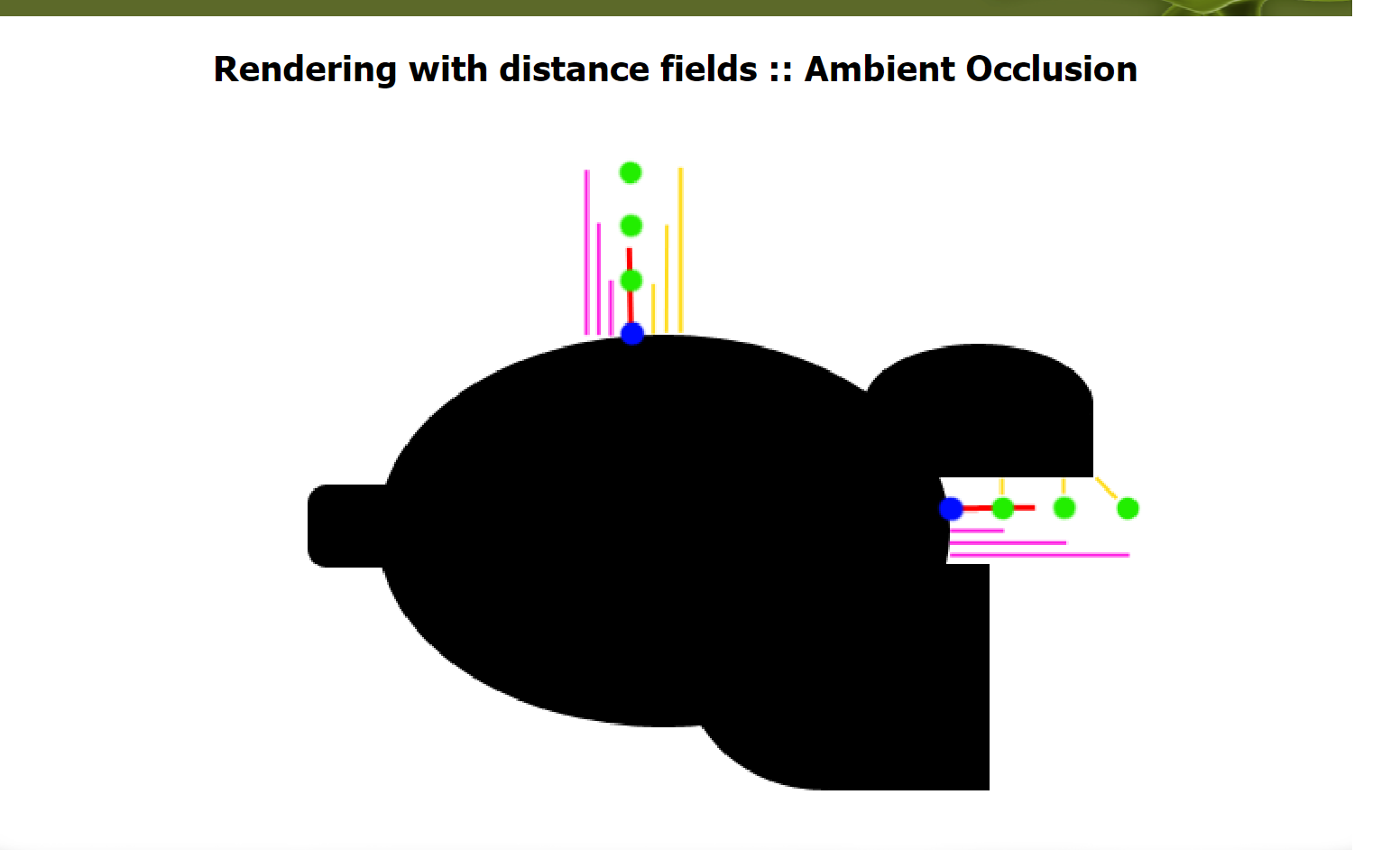

float calcAO( in vec3 pos, in vec3 nor )
{
float occ = 0.0;
float sca = 1.0;
for( int i=0; i<5; i++ )
{
float h = 0.1 + 0.15*float(i)/4.0;
float d= SDFScene( pos + h*nor );
occ += (h-d)*sca;
sca *= 0.95;
}
return clamp( 1.0 - 1.5*occ, 0.0, 1.0 );
}
可以看到AO代码里还是存在很多Magic number的,比如h作为步长大小,对于不同大小的场景可能需要做相应的改变,参数sca等我也见过其他的取值,都可以尝试....
AO效果:

其实这部分非常非常简单...
核心思想就是把SDF函数的返回值改成一个vec2,x放的是距离,y放的是材质代号,当然也有许多其他的实现,这种个人认为非常好实现。
举个小小小小的例子,对于多物体着色,sdf并函数就可以改成这样
vec2 uSDF(vec2 a,vec2 b){
return a.x < b.x ? a : b;
}
例图:

可以看到,有一个是metal球,另一个是lambertian球
当Ray marching的t大于tmax时,就会停止步进。
但是,对于无限大小的物体,就会出现极其突兀的效果,比如物体在远处的拦腰截断了,这可不行....

我不能接受
这就需要构造一个函数,需要满足:当t在一定范围内时,其大小接近1,当t越来越大时,其大小会慢慢下降到0...
好吧,不卖关子了,这就是个以e为底数的指数函数,通常被用来模拟视线边缘的雾....

完美满足条件

Rendering Worlds With Two Triangles. https://iquilezles.org/articles/nvscene2008/rwwtt.pdf
GPU Gems 2 Chapter 8. Per-Pixel Displacement Mapping with Distance Functions https://developer.nvidia.com/gpugems/gpugems2/part-i-geometric-complexity/chapter-8-pixel-displacement-mapping-distance-functions
distance functions https://iquilezles.org/articles/distfunctions/
smooth minimum - 2013 https://iquilezles.org/articles/smin/
normals for an SDF - 2015 https://iquilezles.org/articles/normalsSDF/
soft shadows in raymarched SDFs - 2010 https://iquilezles.org/articles/rmshadows/