在半球上均匀采样的推导

原创
飞起转圈
2022-05-07
858
计算机图形学

引

    上个星期在做SSAO时遇到了这个问题。众所周知SSAO在最早（就是孤岛危机1那会）是在球上采样的，但这导致了结果非常不正确，不该有遮挡的地方很灰很灰，于是在孤岛危机2时就出现了在半球上采样的改进版。我在shader中写了个特别简单的半球采样，代码大概如下：

vec3 sample_on_hemiSphere(vec3 seed)
{
    
    vec3 randVec3 = vec3(
        hash(seed.x) * 2 - 1,
        hash(seed.y),
        hash(ssed.z) * 2 - 1
    );
    /*
    hash return in (-1,1)
    */
    return normalized(randVec3);
}

    简单来说就是在[-1,1] * [0,1] * [-1,1]的空间上生成了一个随机三维向量，然后再进行归一化。我觉着这应该是个均匀采样吧
    然后我在RT Gem上看到了这个半球均匀采样，Amazing！

    我看了半天没想明白为什么作者说这个式子是uniform的，而且一点都不straightforward。
    幸运的是我在PBRT 13.6找到了答案，这次就记录一下。
    不多说了，开始推导

半球上均匀采样的PDF

    PDF是概率密度函数，CDF是累积分布函数。
    我们使用逆分布函数法生成采样点。我们先想办法拿到PDF。回忆球面积分的知识，在采样域半球上对pdf积分得，$\int P(\omega )d\omega = 1$

补个概率论知识：在pdf的全域上积分为1

    又因为均匀分布的pdf为常数，所以可以得到
$P(\omega)\int d\omega=1$
    则PDF为$P(\omega)=\frac{1}{2\pi}$
    又因为$d\omega=sin\theta d\theta d\phi$
    且$\int P(\omega )sin\theta d\theta d\phi=\int P(\theta,\phi)d\theta d\phi$
    可证得$P(\theta,\phi)=\frac{sin\theta}{2\pi}$

处理二维联合PDF

    对于一个联合二维密度函数p(x,y)，当其x与y独立时，有
$p(x,y)=p(x)p(y)$
    但很可惜，大部分有用的PDF其x与y都不是独立的，这时候我们可以先对其中一个变量积分，求出其边缘概率密度
$p(x)=\int p(x,y)dy$
    可以理解为X的单独的PDF,但准确的说，这代表了X在所有能取到的Y上的密度。
    接着求y的条件概率密度$p(y|x)=\frac{p(x,y)}{p(x)}$
    照着这个思路就可以求出
$p(\theta)=\int_{0}^{2\pi}p(\theta,\phi)d\phi=sin\theta$
$p(\phi|\theta)=\frac{p(\theta,\phi)}{p(\theta)}=\frac{1}{2\pi}$

两种采样方式

    我们要让采样的点符合pdf，就是pdf大的地方采样点多，pdf小的地方采样的点少。
    这就可以引申出来第一种采样方法，拒绝采样(reject sampling)，简单来说，我们在一大片区域中随机取点，落在pdf曲线内就接受，反之拒绝，假设取点是均匀的，那么得到的采样点集必然是符合pdf的。
    这是个对标准正态分布拒绝采样的例子

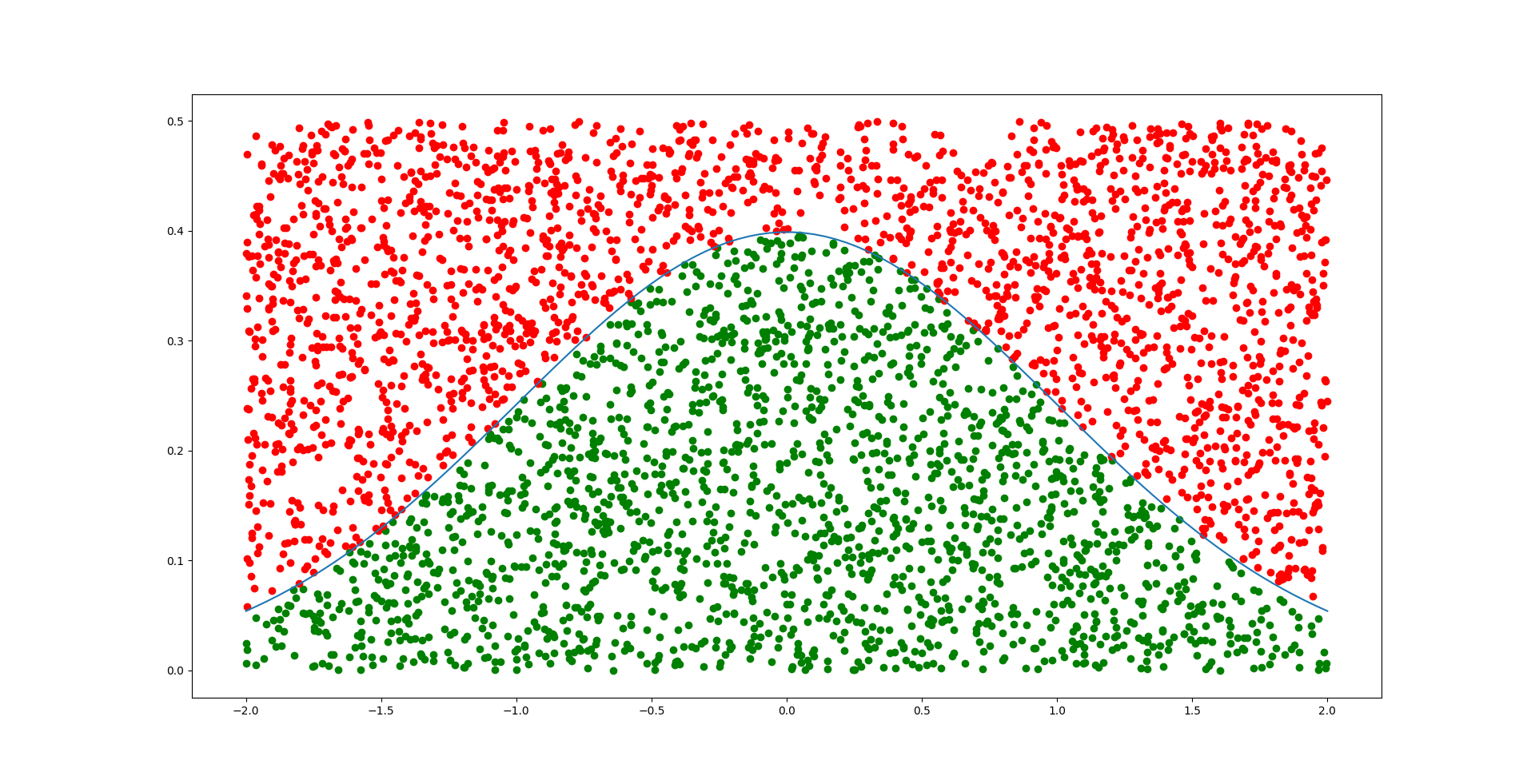
    设随机取到的点为$(x,y)$,如果$y < p(x)$，那么就接受，反之拒绝。
    我选择了[-2,2]*[0,0.5]作为一个大的采样区间，但还是有许多点被拒绝了，显而易见，这与我选上界有关，而且正态分布越两边pdf越小，被拒绝的概率也就越大。
    其实可以把采样的上界换成一个简单，并且恒大于pdf的曲线，这个曲线$q(x)$称为参考函数，则
$\frac{q(x)}{p(x)} = k (k>1)$
    只要两个曲线贴合的比较紧密，就能减少无效的点。
    回到问题上，我们只需要对$\theta,\phi$进行采样，然后根据其与xyz的关系就能拿到坐标了。
    但这样....会不会有点太烦了，即使咋样选择曲线，总是会有无效的点。
    这带来了第二种采样方法，逆变换采样(Inverse transform sampling)
    这种方法需要我们拿到cdf，然后算出反函数，在反函数上取随机点。
    但很可惜许多cdf没有解析解或者即使是计算机算起来也太慢了，举个例子，上过概率论的都记得正态分布的PDF，但谁记得正态分布的CDF呢（笑）。于是只能回到拒绝采样
    证明推导在wiki上，自行查看。
    先对$\phi,\theta$的pdf积分，求出cdf
$P(\theta)=\int_{0}^{\theta}sin\theta d\theta=1-cos\theta\Rightarrow\theta=\arccos(1-\xi_1)$
$P(\phi|\theta)=\int_{0}^{\phi}\frac{1}{2\pi}d\phi=\frac{\phi}{2\pi}\Rightarrow\phi=2\pi\xi_2$
    $\xi_1,\xi_2$为(0,1)上的随机数。
    然后由x,y,z与$\phi,\theta$的关系，我们就能得到这个式子。
$(\sqrt{1-\xi^2} \cos(2\pi\xi_2),\sqrt{1-\xi^2} \sin(2\pi\xi_2),\xi_1)$
    此处用了$\xi_1$代换$\xi_1-1$
    至此推导完毕，如有错误劳烦指出

参考文献

1.Physically Based Rendering-13.6 2D Sampling with Multidimensional Transformations
2.wikipedia-Inverse transform sampling
3.wikipedia-Rejectionsampling

END

留言